
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Superconducting Frame in Magnetic Field
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 76
11-8-2016
2354
Superconducting Frame in Magnetic Field
A superconducting square rigid frame of mass m, inductance L, and side a is cooled down (in a magnetic field) to a temperature below the critical temperature. The frame is kept horizontal (parallel to the x-y plane) and constrained to move in the z direction in a non-uniform but constant
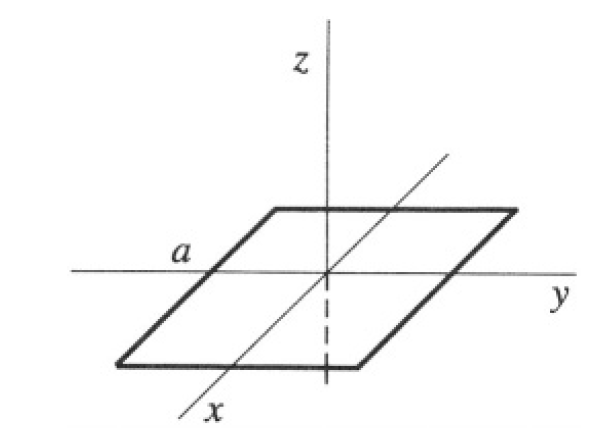
Figure 1.1
magnetic field described by a vector potential A = (-B0 y, αxz, 0) and a uniform gravitational field given by the acceleration g. The thickness of the frame is much smaller than a (see Figure 1.1). Initially, the frame is at rest, with its center coinciding with the origin. Find the equations of motion of the frame and solve for the position of the frame as a function of time.
SOLUTION
Find the magnetic field from the vector potential
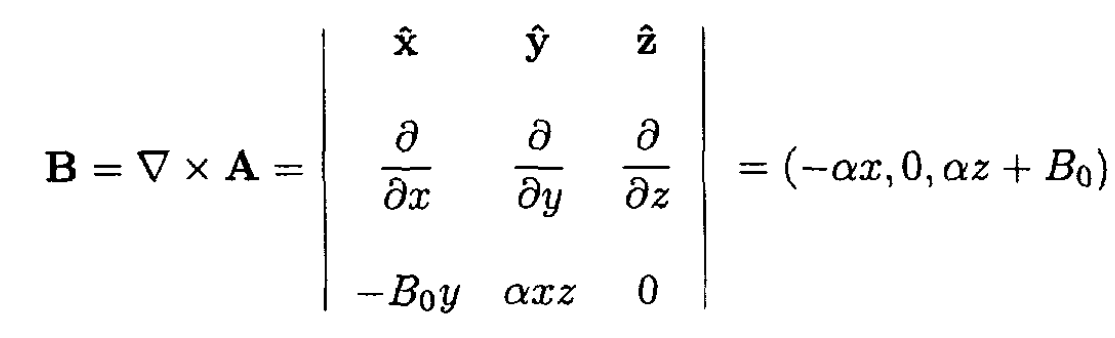
The magnetic flux Φ through the surface of the superconducting frame is constant (see Figure 1.2). Φ is composed of the flux from the external
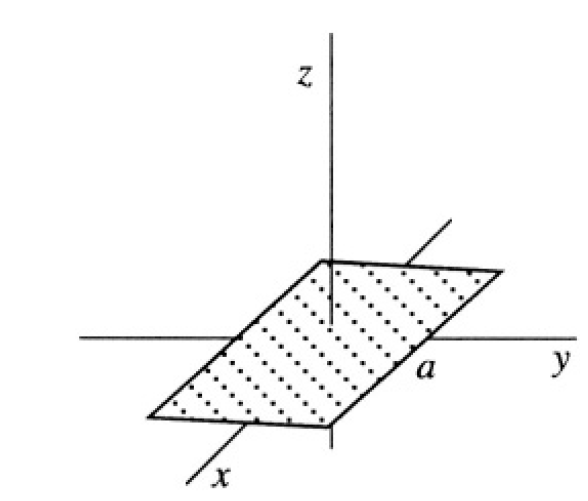
Figure 1.2
magnetic field Φe and the flux Φi produced by the current I flowing in the frame:
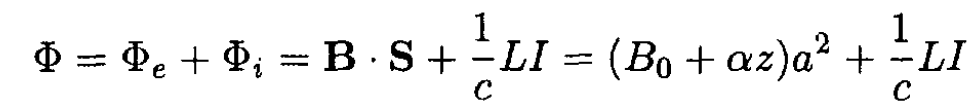
At t = 0, z = 0 and Φ = Φ0 = B0a2. At later times,
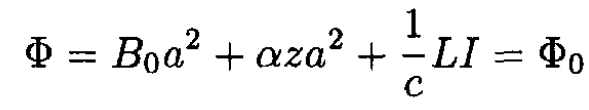
So for the current we have
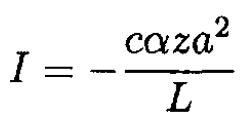
The force on the frame due to the interaction with the magnetic field is given by the general formula
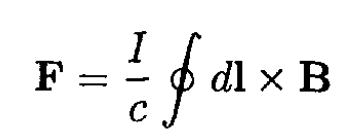
In this problem, due to the physical constraint, we need only the component in the z direction
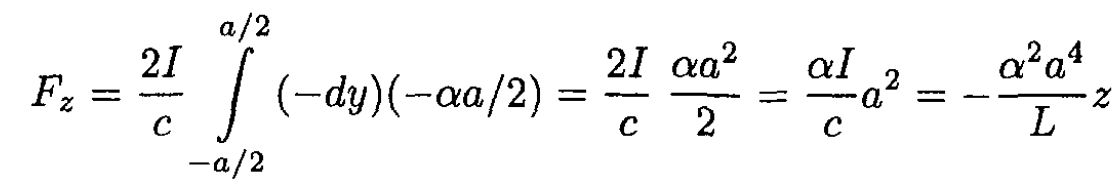
Therefore, the equation of motion becomes
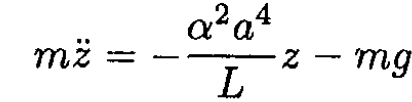
or
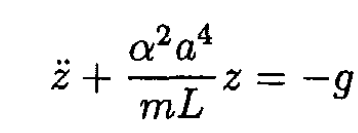
This equation describes oscillatory motion with 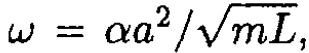 and the solution is
and the solution is
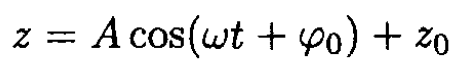
where
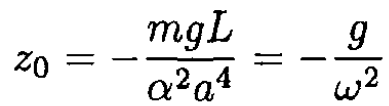
From the initial conditions z(0) = 0 and 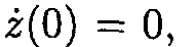 we find that A = -z0 and φ0 = 0. The complete solution for the position of the frame along the z-axis at time t is
we find that A = -z0 and φ0 = 0. The complete solution for the position of the frame along the z-axis at time t is
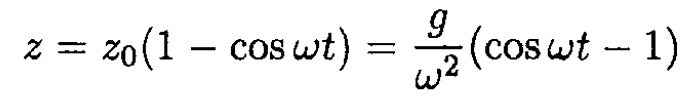
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام) قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)
قسم الشؤون الفكرية يصدر مجموعة قصصية بعنوان (قلوب بلا مأوى)


















