


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 14-8-2016
Date: 2-8-2016
Date: 21-8-2016
|
Unstable Top
A top of mass M is spinning about a fixed point under gravity, and its axis is vertical 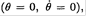 but the angular velocity around its axis ω3 is insufficient for stability in that position. The Lagrangian for a top is
but the angular velocity around its axis ω3 is insufficient for stability in that position. The Lagrangian for a top is
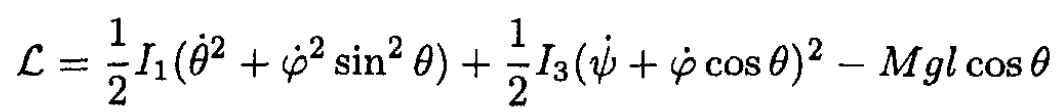
Where θ, φ, ψ are the usual Euler angles, I1 and I3 are the moments of
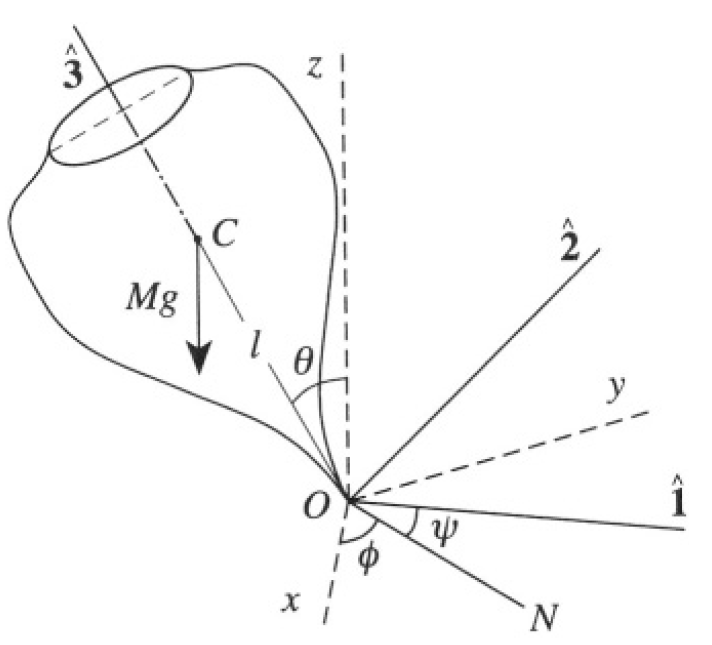
Figure 1.1
inertia about their respective axes, N is the line of nodes, and l is the distance from the point of the top O to the center of mass C (see Figure 1.1).
a) Derive all the first integrals of the motion and evaluate them in terms of the given initial conditions.
b) Show that the head will descend to an angle θ given by
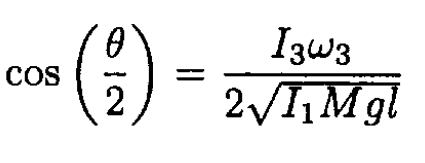
c) Show that the time dependence of this θ is given by the solution of
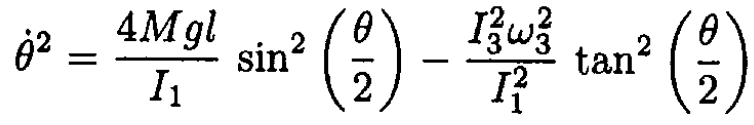
You do not need to solve for θ(t).
SOLUTION
a) There are two integrals of motion in the generalized momenta pφ, pѱ
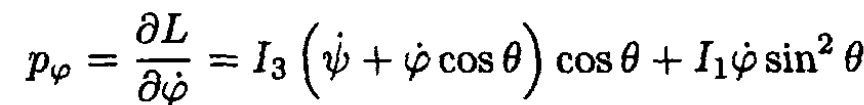 (1)
(1)
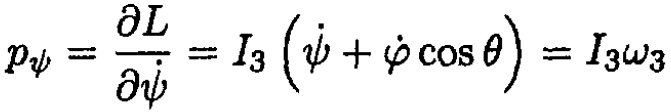 (2)
(2)
where we used the fact that 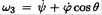 is the angular velocity of the top around its axis. Applying the initial conditions
is the angular velocity of the top around its axis. Applying the initial conditions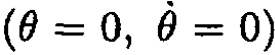 to (1) and (2), we obtain
to (1) and (2), we obtain
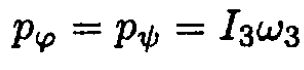
Another integral of motion is, of course, the energy; again using the initial conditions, we have
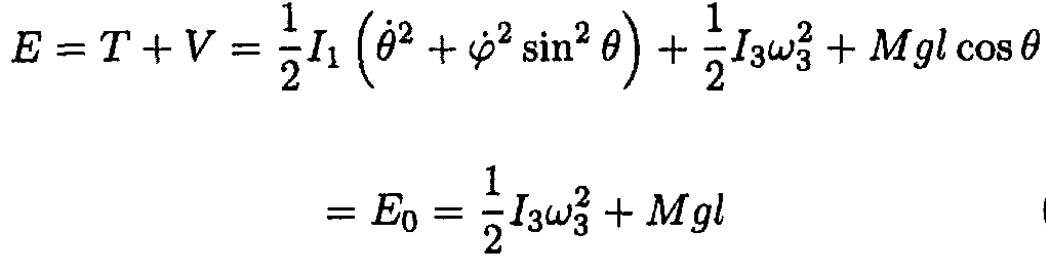 (3)
(3)
b) From (3) and using the condition that the head will descend to a maximum angle θ where 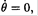 we have
we have
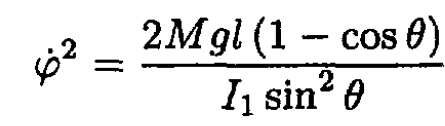 (4)
(4)
On the other hand, from (1),
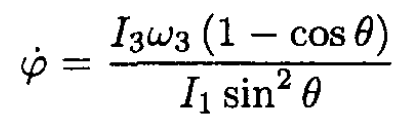 (5)
(5)
By equating 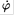 in (4) and (5) and using the half angle formulas
in (4) and (5) and using the half angle formulas
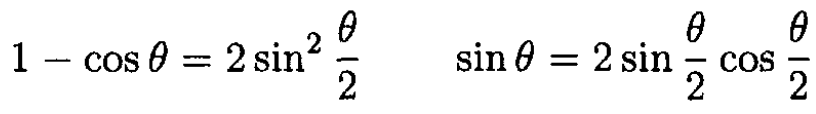
we get
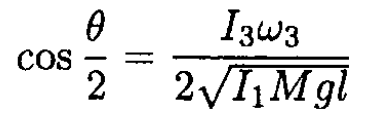
c) Again using (3) and (5), we have
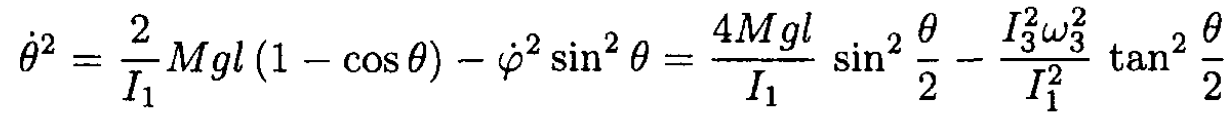



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|