Pendulum Clock in Non-inertial Frame

An off-duty physicist designs a pendulum clock for use on a gravity-free spacecraft. The mechanism is a simple pendulum (mass m at the end of a massless rod of length l) hung from a pivot, about which it can swing

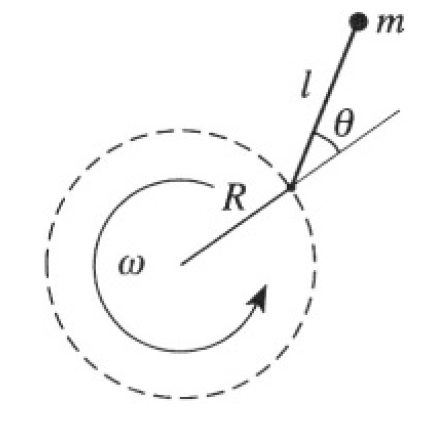
Figure 1.1 

in a plane. To provide artificial gravity, the pivot is forced to rotate at a frequency ω in a circle of radius R in the same plane as the pendulum arm (see Figure 1.1). Show that this succeeds, i.e., that the possible motions θ(t) of this pendulum are identical to the motions θ(t) of a simple pendulum in a uniform gravitational field of strength g = ω²R, not just for small oscillations, but for any amplitude, and for any length l, even l > R.

SOLUTION

Calculate the Lagrangian of the mass m and derive the equation of motion for θ(t) (see Figure 1.2). Start with the equations for the x and y positions of the mass

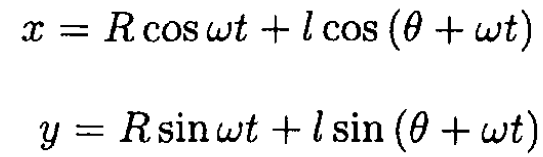
and compose

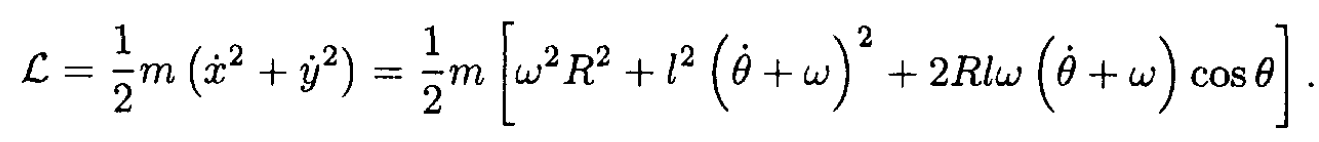
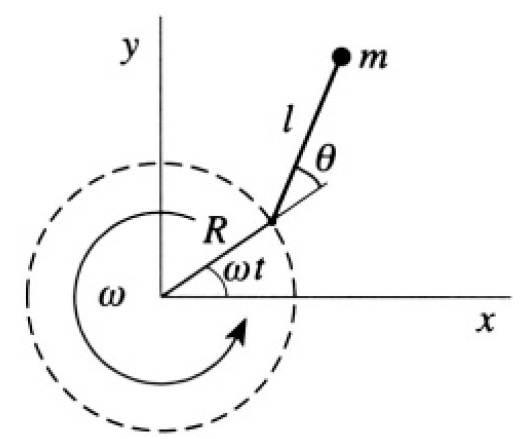
Figure 1.2

Applying Lagrange’s equations gives

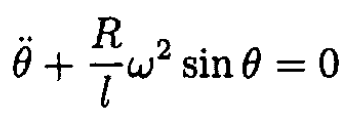
which, for g = ω²R, corresponds, as required, to the equation of motion for a pendulum 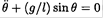 in a uniform gravitational field.