Car down Ramp up Loop

A car slides without friction down a ramp described by a height function h(x) which is smooth and monotonically decreasing as x increases from 0 to L. The ramp is followed by a loop of radius R. Gravitational acceleration is a constant g in the negative h direction (see Figure 1.1).

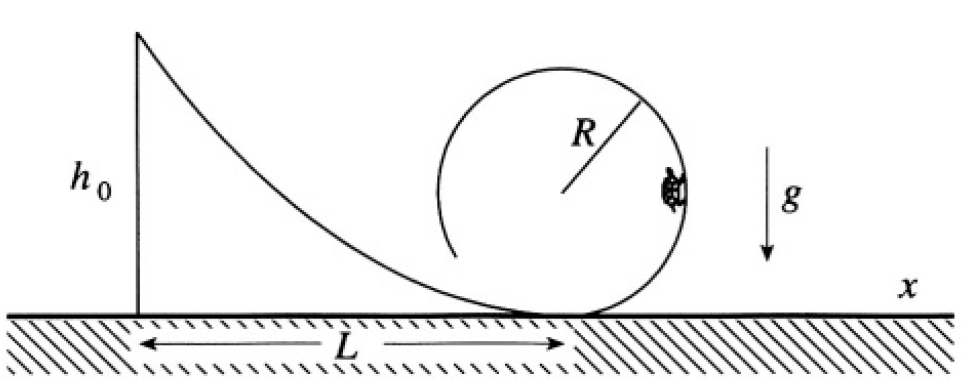
Figure 1.1

a) If the velocity is zero when x = 0, what is the minimum height h₀ = h(0) such that the car goes around the loop, never leaving the track?

b) Consider the motion in the interval 0 < x < L before the loop. Assuming that the car always stays on the track, show that the velocity in the x direction is related to the height as

c) In the particular case that show that the h(x) = h₀[1- sin (πx/2L)] time elapsed in going down the ramp from (0, h₀) to (L, 0) can be expressed as 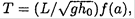  where a ≡ πh₀ /2L, and write f(a) as a definite integral. Evaluate the integral in the limiting case h₀ >> L and discuss the meaning of your answer.

SOLUTION

a) Since there is no friction, we have from energy conservation

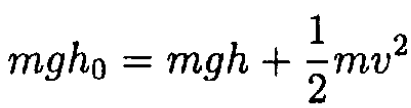
Where v is the velocity of the car and m is its mass (see Figure 1.2). At any point of the ramp, the normal force of the ramp on the car should

Figure 1.2

be nonzero; otherwise, the car will leave the ramp. Obviously, the critical point is the top of the loop, x = L, where the velocity is minimal and gravity and centrifugal forces are antiparallel. For this point,

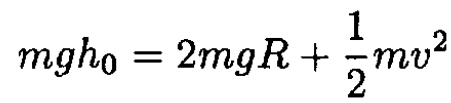 (1)

The minimum height h corresponds to a velocity v = v_min at this point, enough to provide a centrifugal acceleration equal to the gravitational acceleration:

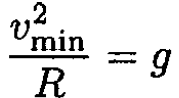
Substituting this into (1) yields

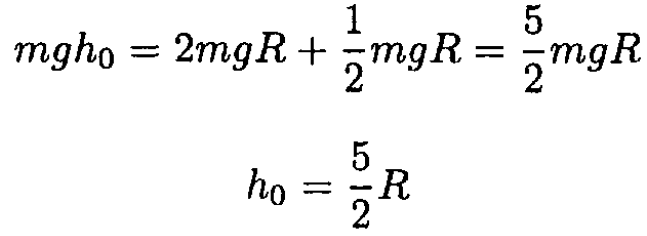
b) Consider a point on the ramp 0 < x < L. The velocity at this point is defined by

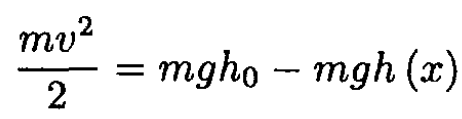(2)

Where v² may be written

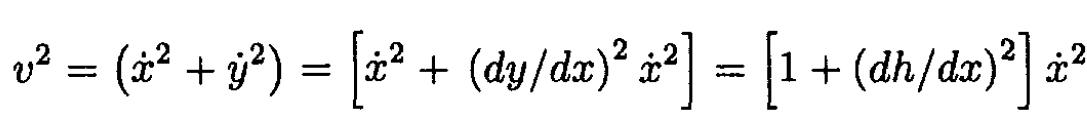 (3)

where the slope of the curve dy/dx is given by the derivative of the height function dh/dx Substituting (3) into (2) results in

c) Now consider h(x) = h₀ [1-sin (πx/2L)]. Rewrite the solution to (b) as

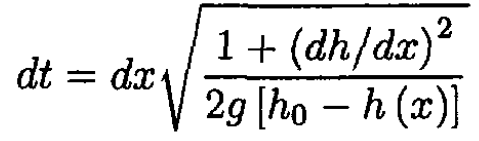
The time T to travel to x = L can be expressed by the integral

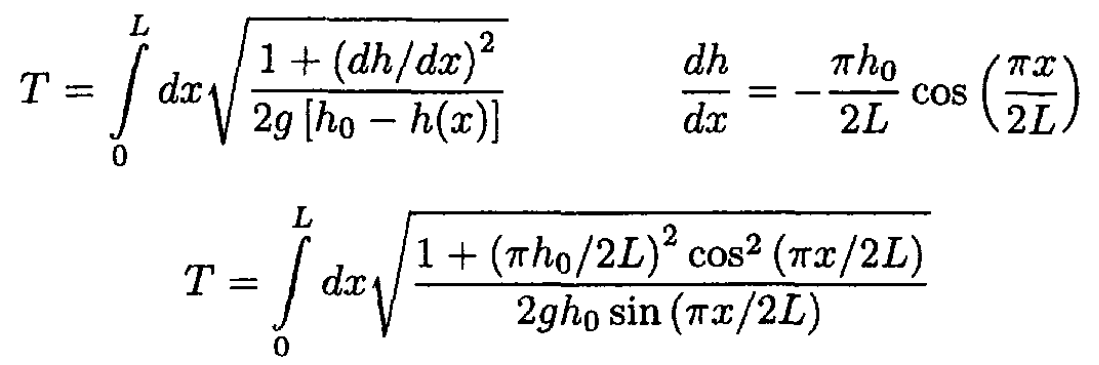
Letting ζ = πx/2L and a ≡ πh₀ /2L, we obtain

where

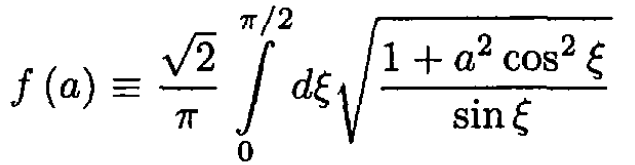
In the limiting case of h₀ >> L, or a << 1, let us write the integral in the form

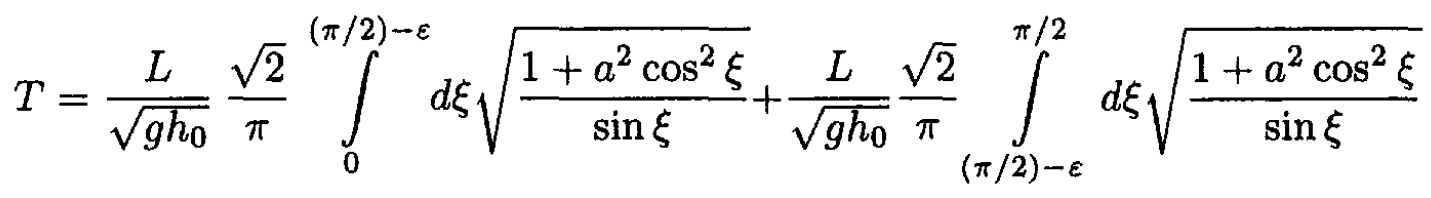
We can neglect 1 compared to a² cos² ζ for the region from 0 to (π/2) – ε, with 1/a < ε << 1. Then we have

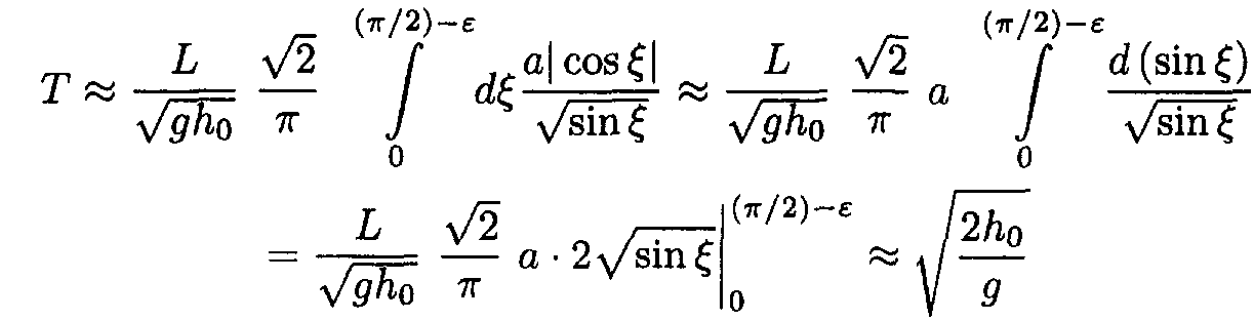
This corresponds to free fall from the height h₀, where gT²/2 = h₀.