Particle in Magnetic Field
المؤلف:
Sidney B. Cahn Boris E. Nadgorny
المصدر:
A GUIDE TO PHYSICS PROBLEMS
الجزء والصفحة:
part 1 , p 31
1-8-2016
1456
Particle in Magnetic Field
a) Give a relationship between Hamilton’s equations under a canonical transformation. Verify that the transformation
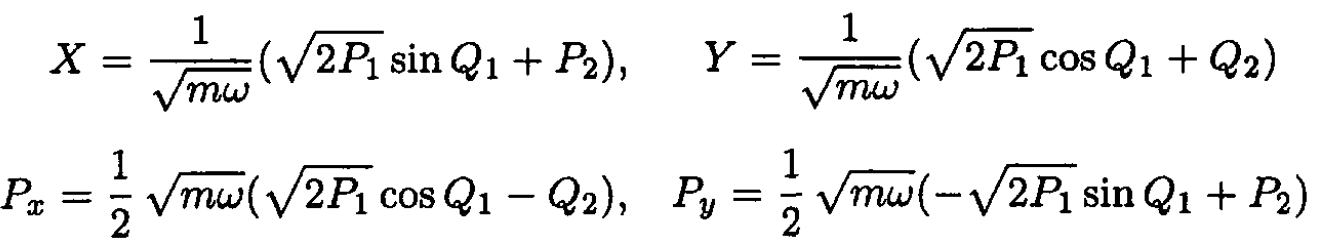
is canonical.
b) Find Hamilton’s equations of motion for a particle moving in a plane in a magnetic field described by the vector potential
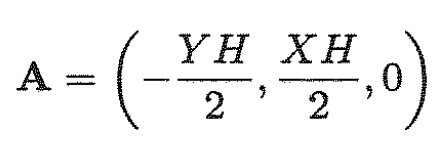
in terms of the new variables Q1, Q2, P1, P2 introduced above, using ω = eH/mc.
SOLUTION
a) A canonical transformation preserves the form of Hamilton’s equations:
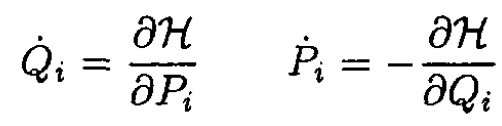
where H = H(Q, P) is the transformed Hamiltonian. It can be shown that Poisson brackets are invariant under such a transformation. In other words, for two functions f, g
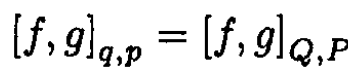(1)
where q, p and Q, P are the old and new variables, respectively. Since we have the following equations for Poisson brackets:
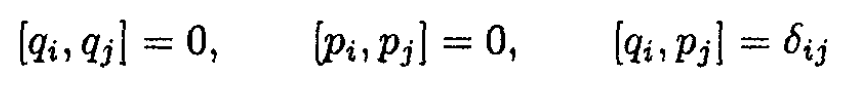(2)
(1) and (2) combined give equivalent conditions for a transformation to be canonical:
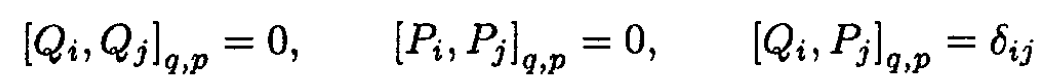
Let us check for our transformation (we let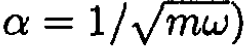
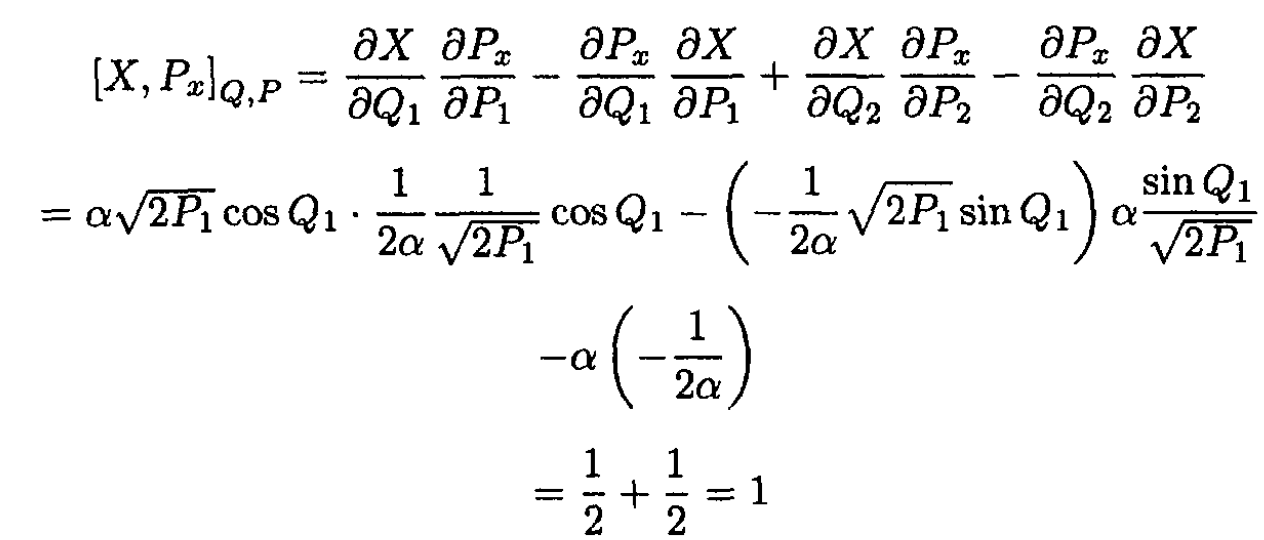
and
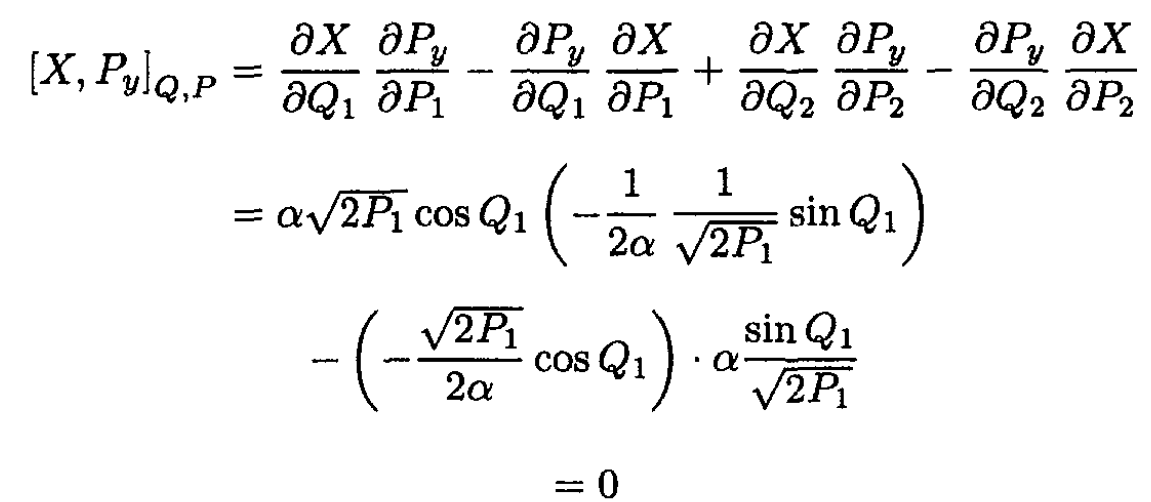
Similarly
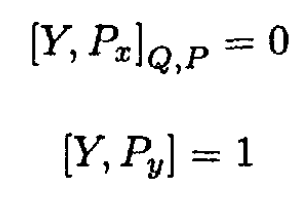
and so on.
For a particle in a magnetic field described by the vector potential A =(–YH/2,XH/2,0), which corresponds to a constant magnetic field
we should use the generalized momentum P in the Hamiltonian
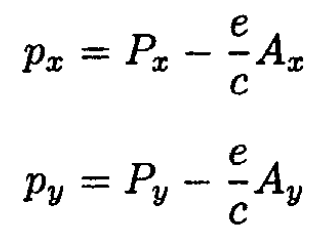
so the Hamiltonian
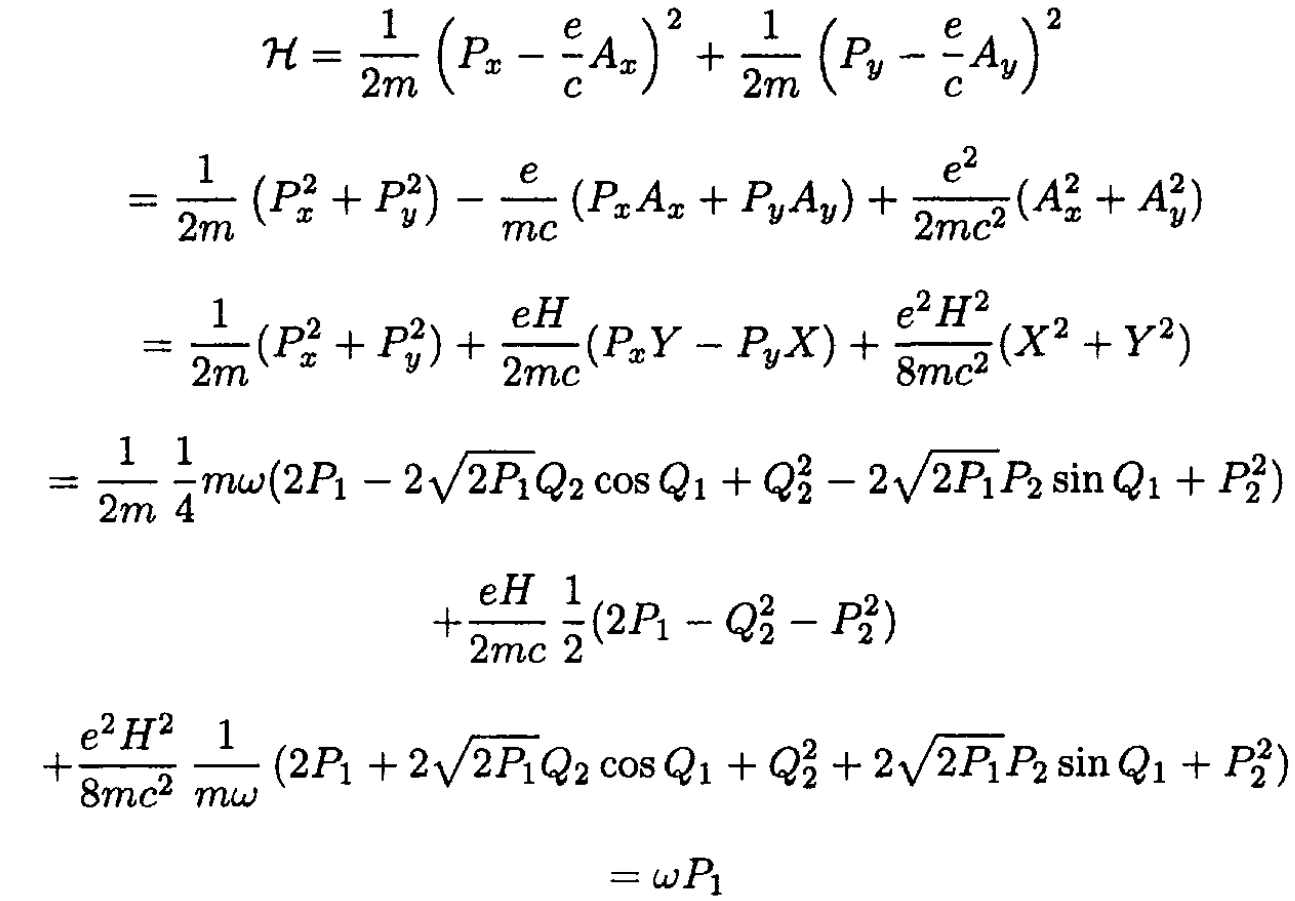
So the Hamiltonian H does not depend on Q1, Q2 and
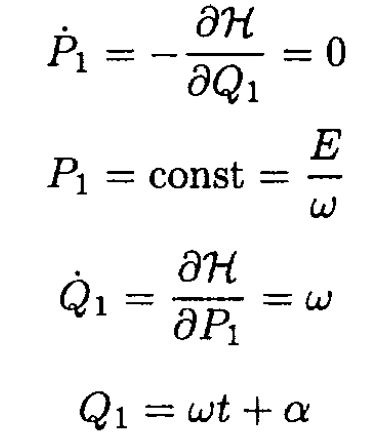
where α is the initial phase. Also
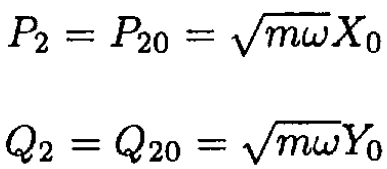
Where X0 and Y0 are defined by the initial conditions. We can write this solution in terms of the variables X, Y, px, py:
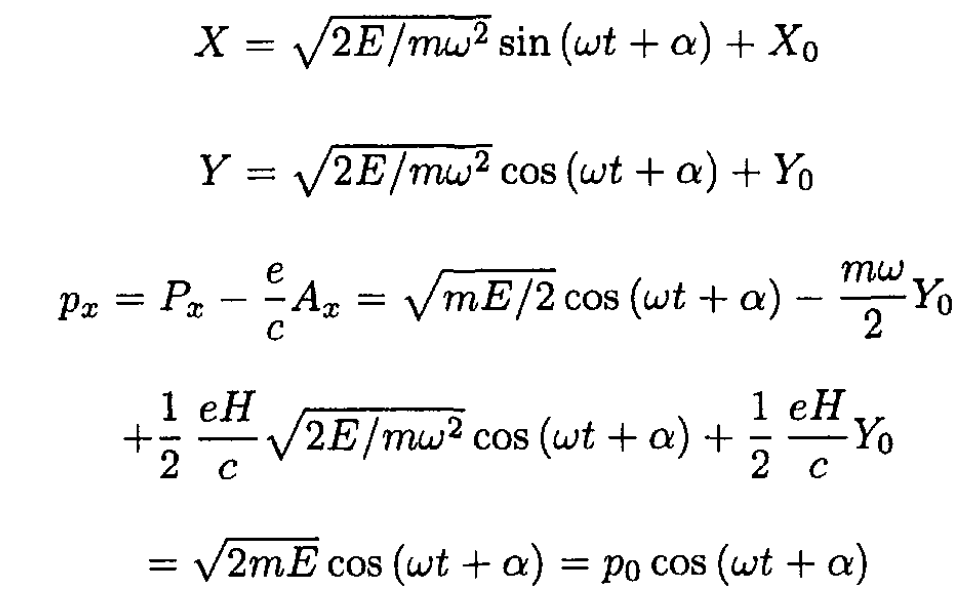
Similarly
so this is indeed the solution for a particle moving in one plane in a constant magnetic field perpendicular to the plane.
الاكثر قراءة في مواضيع اخرى
اخر الاخبار
اخبار العتبة العباسية المقدسة
