Adiabatic Invariants

a) (Adiabatic Invariants) Consider a system with canonical variables

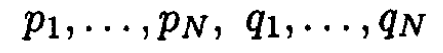
At the time t = 0 let C₀ be an arbitrary closed path in phase space and

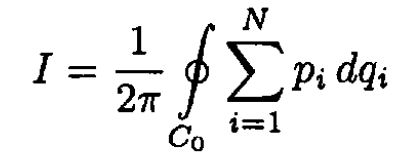
Assume that the point p, q of C₀ moves in phase space according to Hamilton's equations. At a later time the curve C₀ will have become another closed curve C_t. Show that

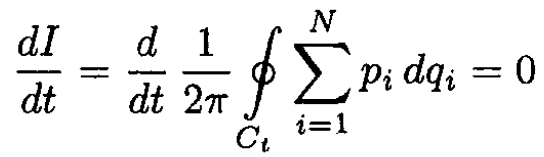
and, for a harmonic oscillator with Hamiltonian H = (p²/2m) + (mω²q²/2) show that

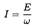
along a closed curve H = (p, q) = E.

b) (Dissolving Spring) A mass m slides on a horizontal frictionless track. It is connected to a spring fastened to a wall. Initially, the amplitude of the oscillations is A₁ and the spring constant of the spring is K₁. The spring constant then decreases adiabatically at a constant rate until the value K₂ is reached. (For instance, assume that the spring is being dissolved in acid.) What is the new amplitude?

Hint: Use the result of (a).

SOLUTION

a)

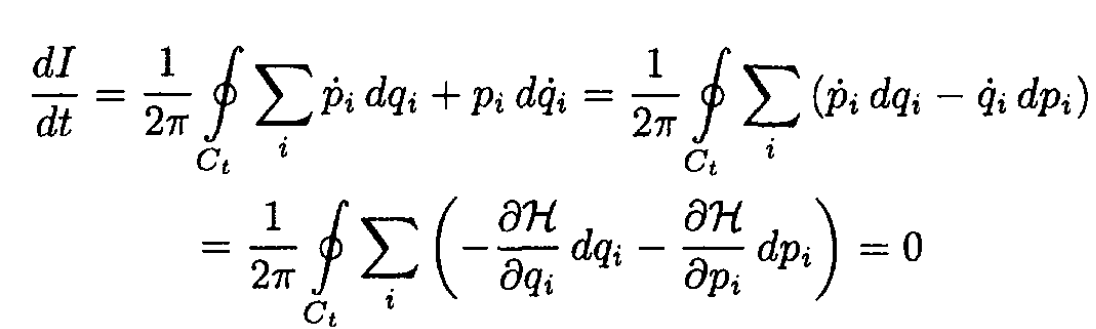
For a harmonic oscillator H(p, q) = E

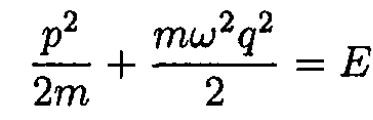
This trajectory in phase space is obviously an ellipse:

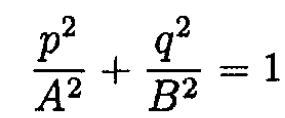
With

(1)

The adiabatic invariant

where we transformed the first integral along the curve into phase area integral which is simply I = σ/2π, where σ is the area of an ellipse σ = πAB So, taking A and B from (1) gives

b) The fact that the spring constant decreases adiabatically implies that although the energy is not conserved its rate of change will be proportional to the rate of change in the spring constant: It can be shown  that in this approximation the quantity found in (a)—the so-called adiabatic invariant—remains constant. Our spring is of course a harmonic oscillator with frequency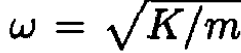 and energy E = (1/2)KA² So we have

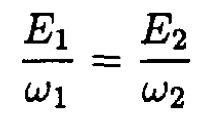(2)

or

So from (2), the new amplitude is