رتبة المصفوفات بعد الفضاء الصفري:

في هذا البند سنركز اهتمامنا على العلاقات بين أبعاد فضاء الصفوف وفضاء الأعمدة والفضاء الصفري لمصفوفة ما ومنقولاتها للاستفادة منها في المواضيع القادمة.

تعريف(1-1):

لتكن A مصفوفة ما. البعد المشترك لفضاء الصفوف وفضاء الأعمدة يقال له رتبة A [يكتب بالرمز rank (A)]. اما بعد الفضاء الصفري للمصفوفة A فيسمى صفرية A [يرمز له   nullity  (A) ].

إذا كانت A مصفوفة و A^T منقولتها فإننا نحصل على ست من فضاءات المتجهات وهي:

1. فضاء صفوف A

2. فضاء أعمدة A

3. الفضاء الصفري إلى A

4. فضاء صفوف A^T.

5. فضاء A^T الصفري.

وبما أن منقولة المصفوفة A تحول متجهات صفوف A إلى متجهات أعمدتها ومتجهات أعمدتها إلى متجهات صفوفها فإن فضاء صفوف A^T هو نفسه فضاء أعمدة A وفضاء أعمدة A^T هو نفسه فضاء صفوف A.

عليه فإننا سنركز اهتمامنا على الفضاءات الأربعة الآتية فقط:

1. فضاء صفوف A.

2. فضاء A الصفري

3. فضاء صفوف A^T

4. فضاء A^T الصفري.

ملاحظة:

فضاءات المصفوفة أعلاه تسمى الفضاءات الأساسية. إذا كانت سعة A هي m x n فإن فضاء صفوف A الصفري هي فضاءات جزئية في Rⁿ . كذلك فضاء صفوف A^T وفضاء A^T الصفري هي فضاءات جزئية في R^m.

مبرهنة (1-2):

لتكن A مصفوفة ما، فإن بعد فضاء صفوف A يساوي بعهد فضاء أعمدة A.

البرهان:

نفرض أن الشكل المدرج الصفي المختزل للمصفوفة A هي R فإن من الملاحظة (1) بعد المبرهنة (5-4-4):

بعد فضاء صفوف A = بعد فضاء صفوف R

كذلك:

بعد فضاء أعمدة A = بعد فضاء أعمدة R

ولما كان: بعد فضاء صفوف R = بعد فضاء أعمدة R.

إذن: بعد فضاء صفوف A = بعد فضاء أعمدة A.

مثال(1):

أوجد رتبة وتصفير A حيث:

باستخدام عمليات الصف البسيطة سنحصل على (تأكد من ذلك بنفسك) الشكل المدرج الصفي المختزل الآتي:

بما أننا حصلنا على ثلاث صفوف غير صفرية، (بمعنى آخر ثلاث أدلة 1) فإن رتبة A تساوي3.

لإيجاد تصفير A فإننا يجب أن نحصل على بعد فضاء حل النظام الخطي AX = 0 وللحصول على هذا الحل فإننا نختزل المصفوفة الممتدة للشكل المدرج الصفي المختزل فنحصل على:

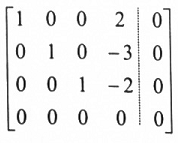
لذا فإن فالنظام الخطي المقابل لهذه المصفوفة هو:

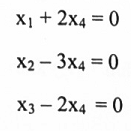
عليه فالحل هو (تأكد من ذلك)

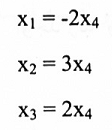
وبفرض x₄ = 1 فإن الحل العام للنظام الخطي AX = 0 هو:

أي أن:

لذا فإن المتجه الوحيد في الجانب الأيمن يكون أساساً لفضاء الحلول وعليه

                                                                   Mull (R) = 1      

مثال(2):

احسب rank (A) وصفرية A إذا كانت:

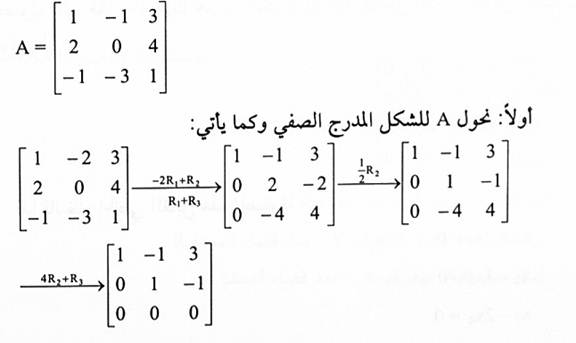
وهذه المصفوفة هي بالشكل المدرج الصفي التي تحوي على صفين مستقلين خطياً. لذا فإن rank (A) = 2                                     

مبرهنة (1-3)                                                 

لتكن A مصفوفة ما، عليه:

                                      (rank (A) = rank (A^T) (اي رتبة A = رتبة A^T)

البرهان:

رتبة A =  بعد فضاء صفوف A = بعد فضاء أعمدة A^T = رتبة A^T

مثال (3):

بالعودة للمصفوفة في المثال 2، أي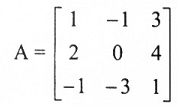 

وبوساطة عمليات الصف البسيطة على A^T نحصل على:

المصفوفة الأخيرة هي بالشكل المدرج الصفي والتي تحتوي على صفين مستقلين خطياً. عليه فإن:

                                                                   Rank (A^T) = 2

وهو نفسه rank (A)

مبرهنة (1-4):

إذا احتوت المصفوفة A على n من الأعمدة فإن:

                                                          Rank (A) + mull (A) = n    

البرهان:

بما أن النظام الخطي AX = 0 له n من المتغيرات وذلك لأن A تحتوي على n من الأعمدة. لذا فإن:

عدد المتغيرات الرئيسية + عدد المتغيرات الحرة = n

لكن عدد المتغيرات الرئيسية هو نفسه عدد الوحدات الرئيسية في الشكل المدرج الصفي المختزل للمصفوفة A وهذا العدد ساوي رتبة [rank (A)] وكذلك لما كان عدد المتغيرات الحرة يساوي صفرية  A  [null (A)] لأن صفرية A هي بعد فضاء الحل للنظام AX = 0 الذي يساوي عدد المتغيرات الوسيطة في الحل العام ويساوي عدد المتغيرات الحرة.

لذا فإن:

بعد فضاء صفوف (أعمدة) A + بعد الفضاء الصفري للمصفوفة n = A

مثال(4):

لما كان بعد فضاء الصفوف في المصفوفة A في المثال 2 يساوي (3) وكذلك بعد الفضاء الصفري يساوي 1، فإن:

4 = 1 + 3 وهو عدد أعمدة A.

أما في المثال 3 فإن بعد فضاء الصفوف هو2  وبعد الفضاء الصفري هو 1، عليه:

3 = 1 + 2 وهو عدد أعمدة A.

مثال(5):

أوجد عدد المتغيرات الوسيطة في حل النظام الخطي AX = 0، غذا علمت أن سعة A هي       5 x 7 وأن رتبة A هي 3 باستخدام مبرهنة (1-3):

صفرية A = (رتبة a) – n = 4 = 7 - 3

Mu₁₁ (A) = n – rank (A) = 7 – 3 = 4

ملاحظة:

لتكن A مصفوفة سعتها m x n ورتبتها r. بوساطة مبرهنة (1-3) سعة A^T هي n x m ورتبتها r. وبوساطة مبرهنة (1-4) فإننا نحصل على:

صفرية A^T تساوي n – r وصفرية A^T تساوي m – r ويمكن تلخيص ذلك بعمل الجدول الآتي:

الفضاءات الأساسية                         بعدها

فضاء صفوف A                            r 

فضاء أعمدة A                               r 

فضاء A الصفري                           n - r

فضاء A^T الصفري                          m - r

إذا كانت A مصفوفة سعتها m x  n فإن متجهات الصفوف تقع في R" ومتجهات الأعمدة تقع في R". من هذا نستنتج أن فضاء صفوف A هو على الأكثر n من الأبعاد وفضاء الأعمدة هو على الأكثر m من الأبعاد. لكن بعد فضاء صفوف A يساوي بعد فضاء أعمدتها. عليه:

إذا كان m ≠ n فإن rank (A) ≤ min (m , n)

مثال(6):

نفرض سعة A هي 7 x 5 لذا فإن رتبة A على الأكثر 5. نستنتج من ذلك أن متجهات الصفوف غير مستقلة خطياً (مرتبطة). كذلك إذا كانت السعة 3 x 6 فإن رتبة A على الأكثر 3 وعليه فإن متجهات الأعمدة غير مستقلة خطياً.

مبرهنة (1-5):

ليكن AX = B نظاماً خطياً يحتوي على m من المعادلات و n من المتغيرات، فإن ما يأتي يكون متكافئاً.

1. AX = B له حل واحد على الأقل (قويم).

2. B داخل فضاء أعمدة A.

رتبة A = رتبة المصفوفة الممتدة [A : B]

البرهان:

2←1 هذا الفرع مبرهن

3←2 بالتعريق، فضاء أعمدة مصفوفة ما هو فضاء متولد من متجهات أعمدتها. لذا فإن فضاءات أعمدة A ,[A : B] متولدة من مجموعتي المتجهات {c₁, c₂, … ,c_n}   و              {c₁, c₂, … , c_n} على التوالي.

 إذا كانت B في أعمدة A فإن أي متجه في المجموعة {c₁, c₂, … , c_n}  و {c₁,c₂,… , c_n, B} هو تركيب خطي للمتجهات {c₁, c₂, … , c_n} وبالعكس. بوساطة مبرهنة (1-6):

نوجد مجموعة جزئية من متجهات أعمدة A التي تكون أساس فضاء أعمدة A. نفرض أن متجهات العمود هذه هي:

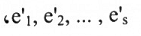، متجهات الأساس هذه تنتمي إلى فضاء الأعمدة ذي البعد s للمصفوفة {A:B] وهذا يعني بأنها تكون أساس فضاء أعمدة المصفوفة [A:B] . هذا يعني أن B هي تركيب خطي من  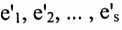وعليه فإن B تقع في فضاء أعمدة A.

مبرهنة (1-6):

ليكن AX = B نظام خطي يحوي m من المعادلات و n من المتغيرات (المجاهيل) فإن العبارات الآتية متكافئة:

1. AX = B قويمة (تحتوي على الأقل حل واحد) لكل مصفوفة B التي سعتها m x  1.

2. متجهات أعمدة A تنشأ R^m.

3. rank (A) = m (رتبة A).

البرهان :

1←2 : من المعادلة 2 بند (5-5) النظام AX = B يمكن التعبير عنه بالصورة:

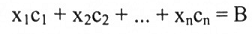
نستنتج من ذلك أنه AX = B قويم لكل B وإذا وفقط إذا كل مصفوفة B يمكن التعبير عنها كتركيب خطي لمتجهات الأعمدة e₁,e₂,……e_n ،بمعنى آخر، إذا وفقط إذا كانت متجهات العمود تنشأ R^m.

1←3 : لما كان AX = B قويماً لكل B وكذلك من 1 و 2 من مبرهنة (1-5) نستنتج أن أي متجه B في R^m يقع في فضاء أعمدة A، أي أن فضاء أعمدة A يقع في R^m . لهذا فإن رتبة A تساوي بعد R^m ، أي يساوي m.

3←1 : بما أن رتبة A تساوي m، فإن فضاء أعمدة A هو فضاء جزئي في R^m بعدة يساوي m وبوساطة مبرهنة (5-4-10) فإنه يساوي كل R^m. من المبرهنة أعلاه ينتج أن AX = B قويماً لكل منتجه B في R وذلك لأن أي متجه مثل B ينتمي إلى فضاء أعمدة A.

ملاحظة:

إذا كان النظام الخطي AX = B يتكون من m من المعادلات و n من المتغيرات بحيث ..... فإن متجهات أعمدة A لا تنشأ R^m . بواسطة المبرهنة أعلاه ينتج أن بالنسبة للمصفوفة A ذات السعة  m x n حيث m>n فإن النظام الخطي AX = 0 ليس قويماً لجميع احتمالات B. على سبيل المثال النظام.

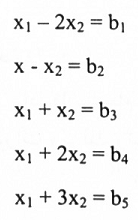
ليس قويماً (m>n) لكل قيم b₁ (1.2.3.4)، المحتملة. والشروط الأساسية لكي يكون النظام قويماً هي بحل النظام بطريقة حذف قاوس ــ جوردن للحصول على الشكل المدرج الصفي للمصفوفة الممتد الآتي:

وهذا الشكل يكون قويماً إذا وفقط إذا حققت b₂, b₄, b₃, b₂, b₁ العلاقات الآتية:

حيث r و s ثوابد لا على التعين.

مبرهنة (1-7):

إذا كان النظام الخطي AX = B قويماً ومتكوناً من m من المعادلات و n من المتغيرات وكذلك رتبة A هي r فإن الحل العام للنظام يحتوي على n –r وسيطاً.

البرهان:

من المبرهنة (1-4) العلاقة 3 الكميات الثابتة c_n, …. , c₂, c₁ هي وسائط الحلول العامة    AX = B  و  AX = 0 لذا فإن هذه الأنظمة تحتوي على نفس العدد من المتغيرات الوسيطة في حلولها العامة، إضافة لذلك ومن برهان مبرهنة (5-6-4) فإن عدد المتغيرات الوسيطة هو null(A) . ومن هذه الحقائق وبوساطة مبرهنة (5-6-4) نحصل على البرهان.

مثال(7):

لتكن A مصفوفة سعتها 4 x 7 ورتبتها 3. وإذا كان النظام الخطي قويماً فإن الحل العام للنظام يحتوي على 7 -3 = 4 وسيطاً.

مبرهنة (1-8):

لتكن A مصفوفة سعتها m x n فإن ما يأتي يكون متكافئاً.

1. النظام الخطي AX = 0 يحتوي على حل وحيد هو الحل الواضح.

2. متجهات أعمدة A تكون مستقلة خطياً.

3. النظام الخطي AX = B يحتوي على الأكثر حلاً واحداً لكل B ذات السعة m x 1.

البرهان:

2←1 نفرض أن . c_n, …. , c₂, c₁ هي متجهات أعمدة A، عليه فإن النظام الخطي AX = 0 يمكن كتابته بالشكل:

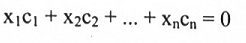
إذا كانت c_n, …. , x₂, c₁ مستقلة خطياً. فإن المعادلة أعلاه تتحقق فقط عندما                                      X₁ = X₂ = …. = X_n =0، وهذا يعني أن الحل الواضح هو الحل الوحيد للنظام AX = 0 وبالعكس، إذا كان الحل الواضح هو الحل الوحيد للنظام AX = 0 فإن المعادلة أعلاه تتحقق فقط عندما x₁ = x₂ = … = c_n = 0 وهذا يعني أن c_n, …. , c₂, c₁ مستقلة خطياً.

1←3: نفرض أن الحل الواضح هي الحل الوحيد للنظام AX = 0 فإن النظام AX = B اما ـن يكون قويماً أو لا يكون ، فإذا لم يكن قويماً فسوف لا يكون للنظام حلاً. اما إذا كان قويماً، نفرض أن x هو حل ما لا على التعيين. من خلال مبرهنة (5-5-4) العلاقة (3) وحقيقة أن الحل الواضح للنظام AX = 0 هو الحل الوحيد نستطيع الاستنتاج بأن الحل العام للنظام AX = B هو:

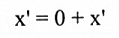
لذا فإن x' هو الحل الوحيد للنظام AX = B

3←1 : نفرض أن النظام AX = B له على الأثر حل واحد ، لكل B سعة m x 1 لذا فإن  AX = 0 له على الأثر حل واحد هو الحل الواضح.

مثال(8):

إذا كانت المصفوفة A ذات سعة 5 x 7 فإن النظام AX = B يكون قويماً لكل B ذات السعة      7 x 1 وأن الحل العام يحتوي على 7 – r من المتغيرات الوسيطة حيث r رتبة A.

ملاحظة:

خلاصة القول نستطيع الآن جمع معظم النتائج المهمة التي حصلنا عليها سابقاً

لتكن A مصفوفة سعتها n x n ونفرض أنها مضروبة التحويلة فإن النتائج الآتية تكون متكافئة:

1. A قابلة للانعكاس.

2. الحل الوحيد للنظام الخطي AX = 0 هو الحل الصفري.

3. الصيغة المدرجة الصفية المختزلة للمصفوفة A هي I_n.

4. A هي عبارة عن حاصل ضرب مصفوفات بسيطة.

5. النظام الخطي AX = B قويماً لكل B مصفوفة سعتها n x 1.

6. يكون للنظام الخطي AX = 0 حلاً وحيداً لكل B.

7. |A| ≠ 0.

8. مدى T_A هو Rⁿ.

9. التحويلة  T_A متباينة.

10. متجهات أعمدة A مستقلة خطياً.

11. متجهات صفوف A مستقلة خطياً.

12. متجهات أعمدة A تنشأ R".

13. متجهات صفوف A تنشأ R".

14. متجها أعمدة A أساس R".

15. متجهات صفوف A أساس R".

16. رتبة A تساوي n.