

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
فضاء الضرب الداخلي-المصفوفات المتعامدة، تبديل الأساسات
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
337-343
15-3-2016
13843
المصفوفات المتعامدة، تبديل الأساسات:
نتناول في هذا البند دراسة العلاقة بين مفهوم الأساس ومصفوفة الإحداثيات، وسندرس أيضاً طريقة تبديل أساسات فضاء المتجهات.
تعريف ((1-1:
يقال للمصفوفة المربعة A متعامدة إذا تحققت العلاقة:
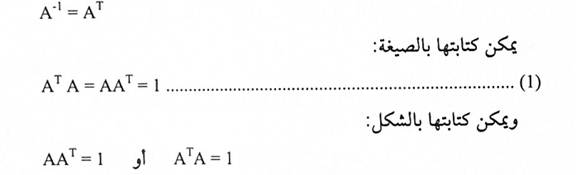
مثال(1):
برهن أن 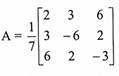 مصفوفة متعامدة. اوجد A-1.
مصفوفة متعامدة. اوجد A-1.
لما كان:
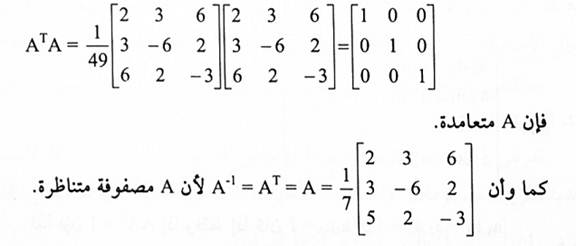
مثال(2):
المصفوفة الأساسية لدوران R2 حول زاوية قيمتها θ هي:
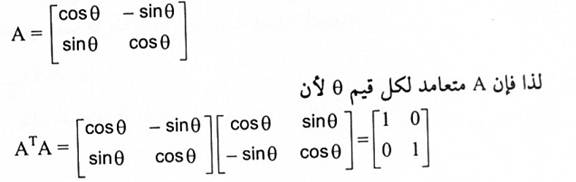
مبرهنة (1-2):
لتكن A مصفوفة سعتها n x n فإن الصيغ الآتية تكون متكافئة.
1. A متعامدة.
2. متجهات صفوف A تكون مجموعة عيارية في R" مع الضرب الداخلي الاقليدي.
3. متجهات أعمدة A تكون مجموعة عيارية في R" مع الضرب الداخلي الاقليدي.
البرهان: 1←2
العنصر في الصف i والعمود رقم j في حاصل الضرب AAT هو الضرب النقطي للمتجه في الصف i من A والمتجه العمود رقم j في AT. لكن متجه العمود رقم j في AT هو نفسه متجه الصف رقم j في A. لذا إذا كانت an, … , a2, a1 هي متجهات صفوف A فإن الضرب AAT يمكن كتابته بالشكل:
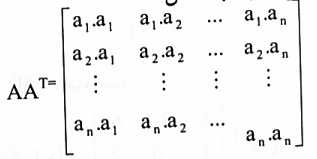
لذا فإن AAT = 1 إذا وفقط إذا كان 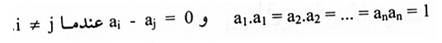 ،هذه العلاقات تكون صحيحة إذا وفقط إذا {a1, a2, …, an} مجموعة عيارية في Rn.
،هذه العلاقات تكون صحيحة إذا وفقط إذا {a1, a2, …, an} مجموعة عيارية في Rn.
بنفس الأسلوب نبرهن 1←3
خواص المصفوفات المتعامدة:
إذا كانت A و B مصفوفتان متعامدتان فإن:
1. معكوس A مصفوفة متعامدة.
2. A B مصفوفة متعامدة.
3 det A = 1 أو det A = -1
البرهان:
1. بما أن A متعامدة فإن AT = A-1 لهذا فإن A-1 متعامدة.
2. لدينا AT = A-1 و BT = B-1 عليه:
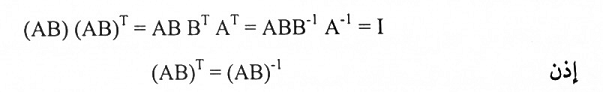
ومن هذا نستنتج ان AB متعامدة.
3. لدينا AAT = 1
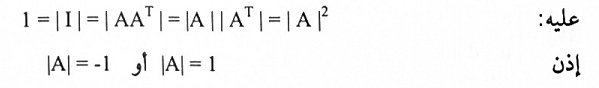
تبديل الأساسات
سنكتفي بشرح طريقة تبديل الأساسات في فضاء البعد الثاني ومن ثم نعمم تلك الطريقة للبعد n.
نفرض v1, v2}=S هي مجموعة الأساس القديم و v'1 , v'2}=S' الأساس الجديد. لإيجاد مصفوفات الإحداثيات لمتجهات الأساس الجديد نسبة للأساس القديم نفترض أن 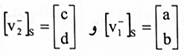 أي أن:
أي أن:

ولكي نجد إحداثيات المتجه v القديمة نكتب v بدلالة الأساس S نعوض (2) في (3) سنحصل على:

أي ان مصفوفة الإحداثيات القديمة s[v] تساوي حاصل ضرب مصفوفة الإحداثيات الجديدة بالمصفوفة 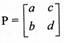 من جهة اليسار حيث أعمدة P هي إحداثيات متجهات الاساس الجديد نسبة للأساس القديم.
من جهة اليسار حيث أعمدة P هي إحداثيات متجهات الاساس الجديد نسبة للأساس القديم.
وبصورة عامة:
إذا نقلنا أساس فضاء المتجهات V من الأساس القديم v1, v2, …, vn}=S إلى الأساس الجديد {v'1, v'2, …. , v'n} S' = فإن مصفوفة الإحداثيات القديمة S[v] للمتجه v يمكن ربطها بمصفوفة الإحداثيات الجديدة s'[v] لنفس المتجه v بواسطة العلاقة:

حيث أن أعمدة P هي مصفوفات إحداثيات الأساس، لجديد نسبة للأساس القديم، أي أن أعمدة P هي:
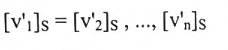
تعريف (1-3):
المصفوفة P التي تنقل الاساس الجديد S' للأساس القديم S تسمى مصفوفة انتقال S' إلى S ويعبر عنها كمتجهات أعمدة بالشكل:

مثال(3):

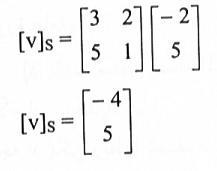
مثال(4):
إذا كانت v'2, v'1, v2, v1 كما في المثال(3) فما هي مصفوفة الانتقال من S' إلى S. من الواضح أن:

خواص مصفوفات الانتقال:
1. إذا ضربنا مصفوفة الانتقال من S إلى S' بمصفوفة الانتقال من S' إلى S نجد أن:
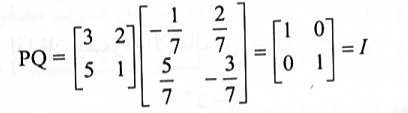
لهذا فإن PQ = 1 أي أن Q = P-1
2. إذا كانت P مصفوفة الانتقال من S' إلى S. فإن لكل متجه v تتحقق العلاقات الآتية:

3. إذا كانت P مصفوفة انتقال من أساس عياري إلى أساس عياري آخر لفضاء الضرب الداخلي، فإن P مصفوفة متعامدة، أي أن P-1 = PT.
مثال(5):
لتكن 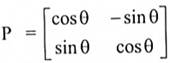 الناتجة من تدوير المحاور y, x بزاوية θ إلى المحاور y' , x'.
الناتجة من تدوير المحاور y, x بزاوية θ إلى المحاور y' , x'.
عليه فإن:
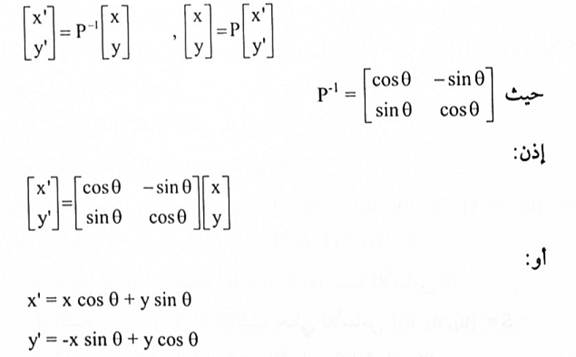
 الاكثر قراءة في الجبر الخطي
الاكثر قراءة في الجبر الخطي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















