

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
193-205
20-3-2016
19828
الفضاء الاقليدي النوني:
تعريف (1-1):
ليكن n عدداً صحيحاً موجباً . المرتبة فئة n من الأعداد الحقيقية (a1, a2, … , an). مجموعة المرتبات فئة n تسمى الفضاء النوني ويرمز له Rm.
عندما n يساوي 2 أو 3 فإننا نطلق التعبير الزوج المرتب أو الثلاثي المرتب بدلاً من المرتب فئة 2 والمرتب فئة 3. من خلال دراستنا للفصل السابق لاحظنا أن الرمز (a1, a2, a3) له تفسيرات هندسية أما يمثل نقطة أحداثياتها a1 و a2 و a3 أو انه متجه مركباته a1 و a2 و a3 لذا من الممكن اعتبار المرتب فئة n (a1, a2, … , an), على أنه تعميم للنقطة أو تعميم للمتجه (شكل 1-1).

شكل ((1-1
تعريف (1-2):
(1) المتجهان v = (v1, v2, … , vn) و u = (u1, u2, …, un) في "R متساويان، إذا كانت مركباتهما المتناظرة متساوية، أي:
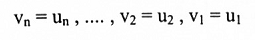
(2) جمع المتجهات v و u، يكتب v + u، هو متجه مركباته عبارة عن جمع مركبات v و u المتناظرة. أي:

(3)ضرب المتجه v بكمية ثابتة k، يكتب kv، هو متجه مركباته هي مركبات v مضروبة في k، أي:

المتجه الصفري في R" يكتب 0 ويعرف (0 = (0, 0, … , 0، إذا كان R"V(v1, v2, …,vn) فإن (-v) هو متجه، يقال له المعكوس الجمعي للمجتهv، ويعرف:

مبرهنة (1-3):
إذا V(v1, v2, …,vn) و u = (u1, u2, …, un) و w = (w1, w2, … , wn) متجهاً في "R.I, k كميات ثابتة، فإن:

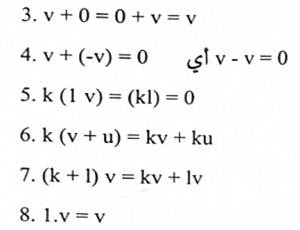
ملاحظة:
بموجب مبرهنة (1-3) يمكن التعامل بالمتجهات من دون استخدام مركباتها، فمثلاً لحل المعادلة x + u = v نضيف النظير –u.
للطرفين:
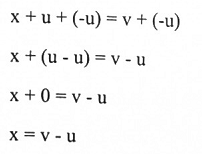
تعريف (1-4)
لتكن V(v1, v2, …,vn) و u = (u1, u2, …, un) متجهان في R". الضرب الداخلي الاقليدي (الضرب النقطي)، يكتب v.u، يعرف:

مثال(1):
لتكن v = (-1,2,3,1) و u = (0,1,2,4) متجهات في R4 فإن:
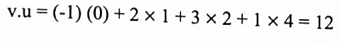
مبرهنة (1-5):
لتكن v و u و w في Rn و k ثابت فإن:

البرهان:
نبرهن 2 و 4.
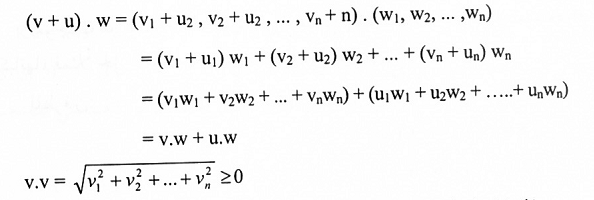
المساواة في الصيغة هذه تكون صحيحة إذا وفقط إذا v1 = v2 = … = 0 إذا وفقط v = 0
تعريف (1-6):

مثال(2): نفرض v = (3,2,1,5) و u = (0,1,-1,3) في R". اوجد طول u والمسافة بينهما.
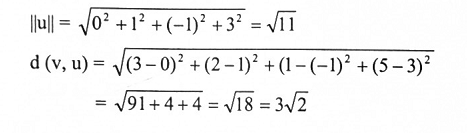
ملاحظة:
يمكن تمثيل المتجه v = (v1, v2, … , vn)في R" بشكل مصفوفة صف أو مصفوفة عمود:

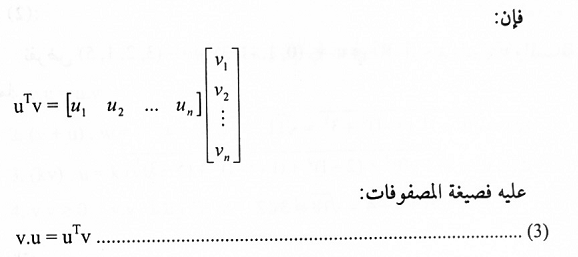
مثال (3):
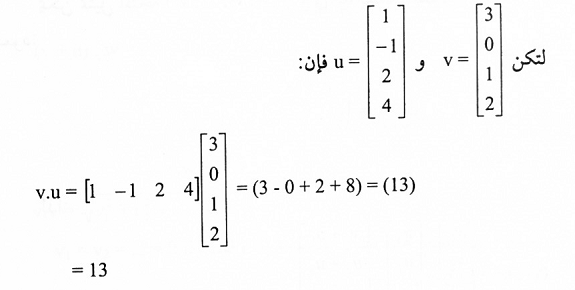
مبرهنة (1-7): (متباينة كوجي ــ شفارتز): لتكن v = (v1, v2, … , vn) و u = (u1, u2, …, un)، فإن:
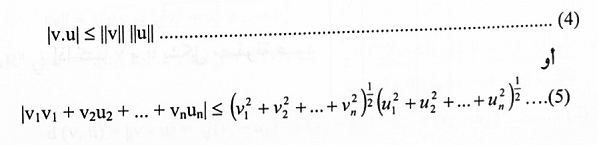
البرهان:
(نبرهن الحالة الخاصة عندما v و u في R2 أما الحالة العامة فسوف نناقشها في المواضيع القادمة).
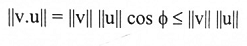
مبرهنة (1-8):
لتكن v و u متهات في R" و k كمية ثابتة، فإن:
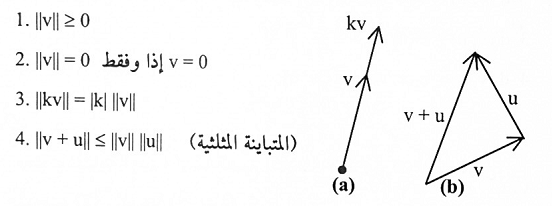
شكل(1-2)
البرهان:
نبرهن الصيغتين (3) و (4)
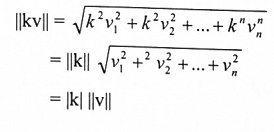
(4) من شكل (1-2) ( b).
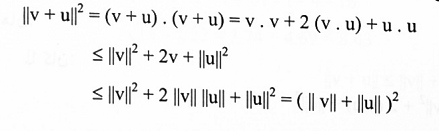
عليه، وبأخذ الجذر التربيعي للطرفين:
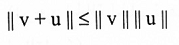
بقية الصيغ نبرهن بنفس الطريقة.
مبرهنة (1-9):
لتكن v و u و w في R" ، k كمية ثابتة، فإن:
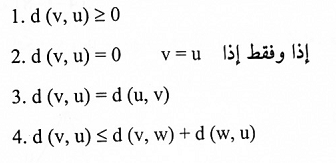
البرهان ستثبت المتباينة (رقم 4). اما الصيغ الثلاث الأخرى، فتترك كتمارين.
بموجب (2) والمبرهنة (1-8) يكون لدينا:
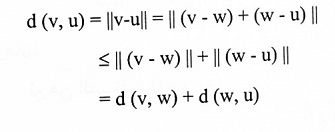
مبرهنة (1-10):
إذا كانت v و ع متجهات في R". فإن:
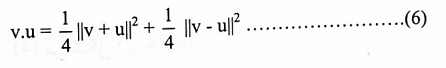
البرهان:
لما كان:
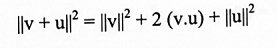
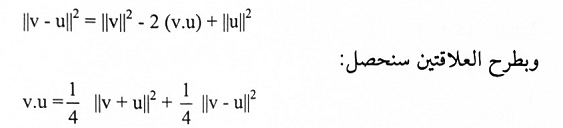
تعريف (1-11):
يقال للمجتهدين v و u في R" بأنهما متعامدان إذا:
v.u = 0
مبرهنة (1-12) (فيثاغورس):
إذا تعامد المتجهات v و u في R" فإن
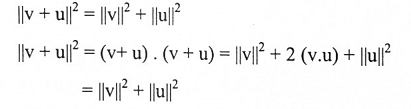
(لأن v و u متعامدان).
مثال(4):
لتكن v و u كما في المثال 3 فإن:


مثال (5):
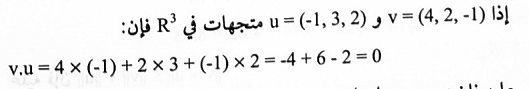
عليه فإن v و u متعامدان.

مثال(6):
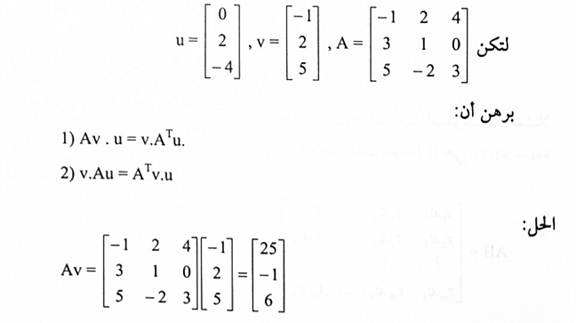

ملاحظة:
الضرب النقطي يساعدنا في تعريف طريقة جديدة لضرب المصفوفات، فمثلاً إذا كانت متجهات صفوف A
هي rn ……, r2,r1 ومتجهات أعمدة B هي cn, … c2, c1 فإن ضرب المصفوفات AB:
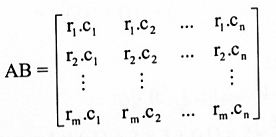
عليه ، فالنظام الخطي AX = B يمكن كتابته بصيغة الضرب النقطي:

إذ أن rn, …. , r2, r1 متجهات صفوف A و bn, … b2, b1 عناصر B.
مثال(7)
اكتب النظام الآتي بشكل ضرب نقطي:
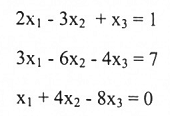
الحل:
بموجب الشكل (1-2):
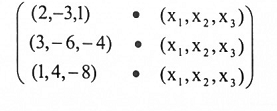
 الاكثر قراءة في الجبر الخطي
الاكثر قراءة في الجبر الخطي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















