


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 20-3-2016
التاريخ: 13-3-2016
التاريخ: 20-3-2016
التاريخ: 6-3-2016
|
الفضاءات الجزئية:
تعريف (1-1):
تسمى المجموعة الجزئية W من الفضاء V، فضاء جزئي في V إذا كانت W نفسها فضاء متجهات تحت عمليتي الجمع والضرب في V.
ملاحظة:
يتضح من التعريف (1-1) أنه لكي نبرهن W فضاء جزئي من V علينا أن نبرهن أن W تحقق الشروط العشرة الواردة في التعريف (1-1)في(فضاء المتجهات الحقيقي). ولكن عدداً من تلك الشروط لا حاجة لتحقيقها هنا لأن W هي جزء من V، هذه الشروط هي m5,m4, m3, m2, A3. لذا سنحتاج فقط برهان الشروط m1, A5, A4, A1.
مبرهنة (1-2):
المجموع الجزئية غير الخالية W من V تكون فضاء جزئي من V إذا وفقط إذا تحقق الشرطان:
1. لكل v,u∊W فإن v+u∊W
2. إذا k عدد ثابت و v ∊W فإن KV∊W
البرهان :
نبرهن الاتجاه الأول.
نفرض W قضاء جزئي، إذن W فضاء متجهات ولهذا فإنها تحقق شروط التعريف (1-1) في(فضاء المتجهات الحقيقي)، ومنها الشرطان 1 و 2.
وبالعكس نفرض الشرطان متحققان.
لما كانت الشروط A2 و A3 و m2 وm3 و m4 و m5 متحققة تلقائياً لأن W مجموعة جزئية من V.
بقي لدينا أن نبرهن الشروط A4 و A5.
نفرض v ∊W ، بموجب الشرط الثاني أعلاه فإن Kv ∊W لكل ثابت K. بفرض K = 0 فإن 0V = 0 (مبرهنة (1-2) في(فضاء المتجهات الحقيقي)، في w وعند فرض K = -1 نحصل على (-1)v = -v في W.
مثال(1):
لتكن w هي مستوى مار بنقطة الأصل [الشكل (1-1) ] و u, v متجهات في W. لذا v+u ∊W وان v + u قطر متوازي الأضلاع، كذلك kv يقع في w ولأي k لأن kv متجه يقع عل امتداد الخط المار بالمتجه v. لذا فإن شروط المبرهنة (1-2) متحققة. عليه فإن W قضاء جزئي.
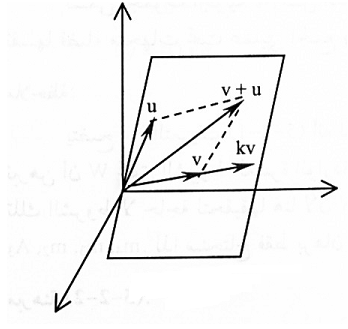
شكل (1-1)
مثال(2):
إذا كانت V فضاء متجهات فإن المجموعة {0} و V نفسها فضاءات جزئية من V، (لأن 0+0=0 وk0=0 لكل عدد ثابت k).
الفضاءات الجزئية {0} و V تسمى الفضاءات الجزئية الواضحة. الفضاءات الجزئية في V عدا الواضحة تسمى الفضاءات الجزئية الفعلية.
مثال(3):
نفرض W هو المستقيم المار بنقطة الأصل في R3، فإن W هو فضاء جزئي. واضح هندسياً [الشكل (5-2) ] أن مجموع متجهين واقعين على هذا المستقيم يقع على المستقيم نفسه، كذلك ضرب أي متجه واقع على هذا المستقيم بعدد ثابت يقع على المستقيم نفسه.
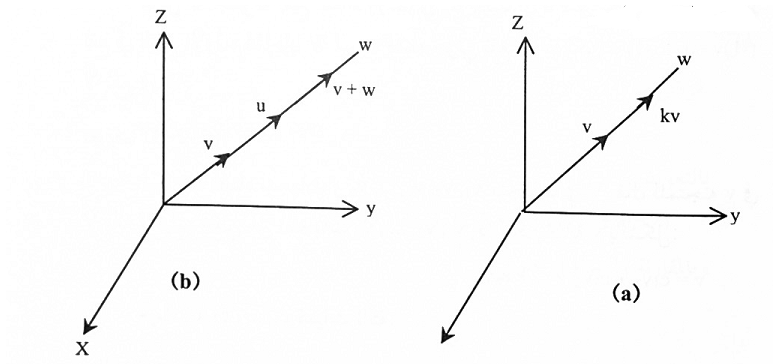
شكل (2-1)
مثال(4):
لتكن Pn مجموعة جمع متعددات الحدود التي درجاتها أصغر أو تساوي n. إذا كان 0<m<n فإن المجموعة الجزئية Pm فضاء جزئي فعلي في Pn .
مثال(5):
إذا كان U و W فضاءات جزئية في الفضاء V فإن تقاطعهما U⋂W فضاء جزئي في V.

مثال(6):
لتكن W مجموعة جميع النقاط (x,y) في R2 بحيث أن x,y≽0 إذن هذه النقاط تقع في الربع الأول، لهذا فإن W ليست فضاء جزئي تقع في W لكن (-1)v=(-1,-1)لا تقع في W.
تعريف (1-3):
ليكن V فضاء متجهات و v1, v2, v3, … , vn متجهات في V يقال للمتجه v في V بأنه تركيب خطي من المتجهات v1, v2, , …, vn إذا أمكن كتابة v بالشكل:
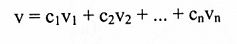
حيث cn, … , c2, c1 كميات ثابتة.
مثال(7):
نفرض v1 = (1,2,-1) و v2 = (1,0,-1) متجهات في R3 ، فإن v = (1,0,2) تركيب خطي من المتجهات v1 و v2.
لكي نبرهن تركيب خطي يجب أن نجد c1 و c2 بحيث v = c1v1 + c2v2 أي أن :

عليه:
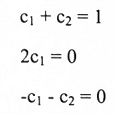
ولكن هذه المعادلات ليست لها حل، عليه فإن v ليست تركيب خطي من v1 و v2.
مثال(8):
إذا كانت  متجهات في R3 فإن v = (2,1,5,-1) هو تركيب خطي من v1 و v2 و v3
متجهات في R3 فإن v = (2,1,5,-1) هو تركيب خطي من v1 و v2 و v3
الحل:
نفرض:
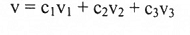
بالتعويض:

وبالمقارنة والتساوي نحصل على:

أي أن:
V=v1+2v2-v3
ومنها فإن v تركيب خطي من v3,v2,v1.
تعريف (1-4):
إذا كانت v1,v2,….vn متجهات في V، وأن أي متجه v في V هو تركيب خطي من v1,v2,….vn ، فإن هذه المتجهات يقال بأنها تكون [أو تولد أو تنشأ] V
مثال (9):
المتجهات القياسية I = (1,0,0) ، j = (0,1,0) ، K = (0,0,1) في R3 تولد (تنشأ) R3 يمكن كتابته بالشكل:
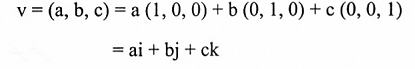
تركيب خطي من k,j,i.
ملاحظة:
إذا كانت Vn, … , V2, v1 تنشأ الفضاء V، فإننا نقول بأنها Span (V).
مثال(10):
xn,….x2,x,1تنشأ فضاء المتجهات Pn مجموعة جميع متعددات الحدود من الدرجة n) وذلك لأن متعددة حدود p∊pn(x) هي عبارة عن تركيب خطيب من xn,….x2,x,1، أي:
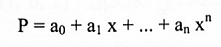
مثال(11):

مبرهنة (1-5):
لتكن S = v1, v2, … , vm مجموعة جزئية من V، فإن:
1. مجموعة جميع التراكيب لمتجهات S، تكتب L(S)، تكون فضاء جزئياً من V.
2. إذا كانت W فضاء جزئي آخر في V يحوي S فإن L(S)CW. بمعنى آخر L(S) هو أصغر فضاء جزئي يحوي S ويسمى الفضاء الجزئي المتولد من S.
البرهان:
1. نفرض أن u, v متجهان في L(S)، أي:
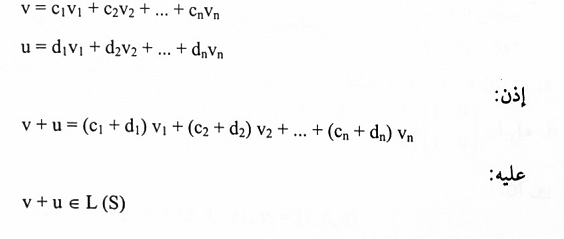
وكذلك:

إذن كل من v + u و kv في L(S). عليه L(S) فضاء جزئي من V. لما كان أي متجه في S يمكن كتابته.
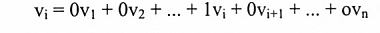
فإن L(S) يحتوي على جميع المتجهات vn, … , v2,v1.
2. نفرض أن W فضاء جزئي يحوي S. لما كان W مغلق بالنسبة للجمع والضرب بكمية ثابتة. لذلك فإن W يحوي على جميع التراكيب الخطية.
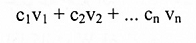
لكل المتجهات vn, …, v2,v1 عليه L(S) CW.
مبرهنة (1-6):
لتكن S = v1, v2, …, vm و S' = v1, v2, …, vn مجموعتان في V، فإن الفضاء الجزئي المتولد بواسطة = S الفضاء المتولد بواسطة S' إذا وفقط إذا كل متجه في S' هو تركيب خطي من متجهات S وبالعكس.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|