

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
المتجهات في فضاء البعد الثاني وفضاء البعد الثالث-الضرب الاتجاهي (الضرب التقاطعي)
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
163-175
7-3-2016
57941
الضرب الاتجاهي (الضرب التقاطعي):
كثيراً من تطبيقات المتجهات في الفيزياء والهندسة تحتاج إلى معرفة المتجه المرسوم في الفضاء 3- الذي يكون عمودياً على متجهين معلومين. سنحاول في هذا البند التعريف بأحد انواع المتجهات الذي يعطينا ذلك المتجه.
تعريف (1-1): لكت v = (v1 , v2 , v3) و u = (u1 , u2, u3) متجهان مرسومان في فضاء 3- فإن الضرب الاتجاهي ،يكتب v x u، يعرف:
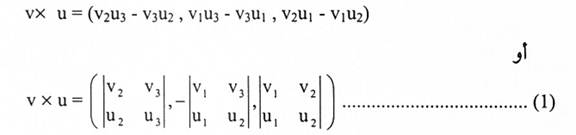
إن حفظ الصيغة اعلاه قد يبدو صعباً، لذا نقترح الطريقة الآتية لإيجاد مركبات v x u.
1. نرتب مركبات v و u بشكل مصفوفة سعتها 2 x 3.
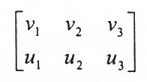
2. نوجد المركبة الاولى للمتجه v x u بحذف العمود الأول ونأخذ محدد المصفوفة الباقية فنحصل على:
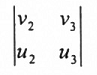
3. نوجد المركبة الثانية للمتجه v x u بحذف العمود الثاني ونأخذ سالب محدد المصفوفة الباقية:

4. نحذف العمود الثالث من المصفوفة الأصلية وبأخذ محدد المصفوفة المتبقية نحصل على:
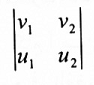
مثال (1):
أوجد v x u إذا علمت ان v = (4-, 0,2) و u = (1,3,-3)
الحل:
نجد مصفوفة مركبات v و u:
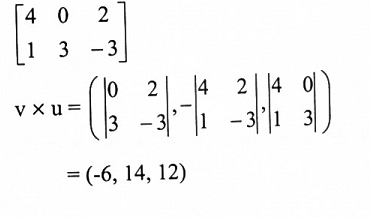
ملاحظة:
الضرب النقطي v.u هو كمية ثابتة بينما الضرب الاتجاهي v x u فهو متجه. كما وأن المتجه v x u عمودي على كل من v و u.
مبرهنة (1-2):
إذا كانت w,u,v متجهات مرسومة في فضاء 3- فإن:
1. v. (v x u) = 0 (v x u عمود على v).
2. u. (v x u) ( v x u عمود على v).

البرهان:
نبرهن الحالة (1)
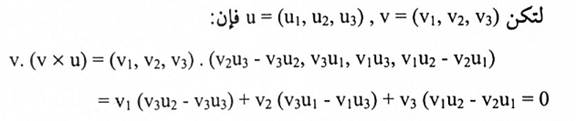
مثال(2):
لتكن v = (2,3,-4) ، u = (1,-1,2) . احسب u x v ثم برهن أن u x v عمودياً على كل من u و v.
الحل:

وبنفس الطريقة v. (u x v) = 0
لذا فإن u x v متجهات في فضاء 3- و k كمية ثابتة فإن:
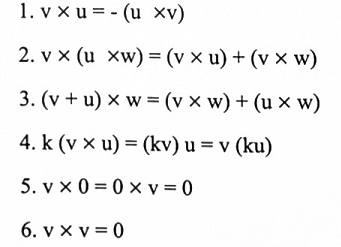
البرهان:
نكتب المصفوفة:

لتكن i = (1,0,0)، j = (0,1,0) ، k = (0,0,1) هذه المتجهات تسمى متجهات الوحدة القياسية في فضاء 3- وتقع على امتداد الإحداثيات الثلاثية (الشكل (3-23). وأن أي متجه مثل v = (v1,v2,v3)يمكن التعبير عنه بدلالة k,j,i وكالآتي:
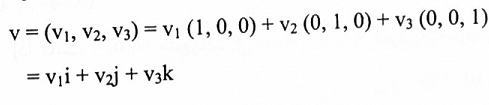

شكل1-1

شكل (1-2)
ولسهولة حفظ هذه العلاقات يمكن تمثيل ذلك باستخدام الشكل (1-2)، حيث أن الضرب الاتجاهي لأي متجهين قياسيين باتجاه عقارب الساعة يساوي المتجه الثالث بإشارة موجبة والضرب عكس عقارب الساعة فيساوي المتجه الثالث بإشارة سالبة.
ملاحظة:
يمكن التعبير عن الضرب الاتجاهي باستخدام k , j , i وكما يأتي:
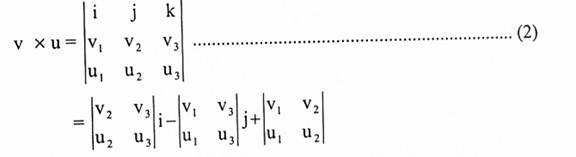
مثال (3):
لتكن v = (1,0,-2) و u = (3,2,1) فإن:
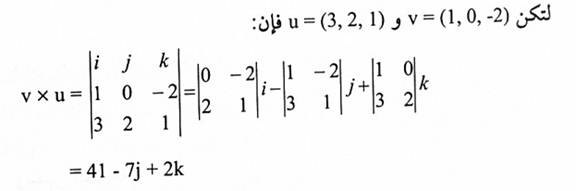
مبرهنة (1-4):
إذا كانت v و u متجهان في فضاء 3-، فإن || v x u|| تساوي مساحة متوازي الأضلاع المتكونة بواسطة v و u.
البرهان:
من المبرهنة (1-2) (3) لدينا:

لكن ||u||sin⍉ هو ارتفاع متوازي الأضلاع المتكون من v و u. لذا فإن مساحته A (شكل 1-3) هي:

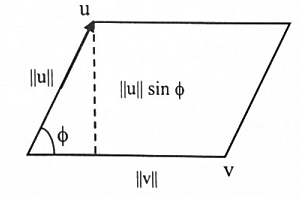
شكل (1-3)
مثال(4):
أوجد مساحة متوازي الأضلاع الذي رؤوسه P = (1,3,-2) ، Q (2,1,4) و R(-3,1,60)
الحل:

شكل (1-4)
تعريف (1-5):
إذا كانت w, u, v متجهات في فضاء 3-، فإن v. (u x w) يقال له الضرب الثلاثي النقطي.
من الممكن إيجاد الضرب الثلاثي النقطي للمتجهات v = (v1, v2, v3) و u = (u1 , u2, u3) و w = (w1 , w2 , w3) من الصيغة:

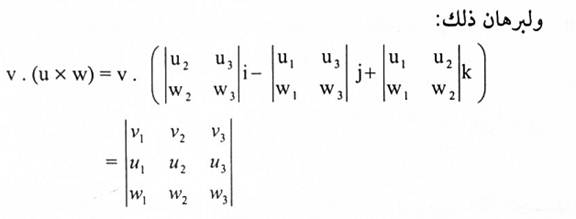
مثال (5):
أوجد الضرب الثلاثي النقطي للمتجهات:

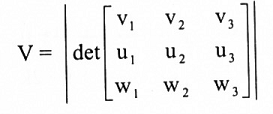
تمرين (1): مساحة متوازي الأضلاع في فضاء 2- المتكون من u = (u1 , u2) و u = (u1 , u2) تساوي القيمة المطلقة للمحدد:

(2) حجم متوازي المستطيلات ف فضاء 3 المتكون بوساطة المتجهات
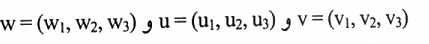
يساوي القيمة المطلقة للمحدد:
الحل:
(1) من الممكن استعمال مبرهنة (1-4) لبرهان الحالة (1) من خلال اعتبار v = (v1 , v2) و u = (u1, u2) متجهات مرسومة ف الفضاء الجزئي xy من النظام الثلاثي الأبعاد xyz (شكل 1-5). في هذه الحالة v = (v1, v2, 0) و (u1, u2, 0). لذا

وبموجب المبرهنة (1-4) وحقيقة كون ||K|| = 1، المساحة A لمتوازي الأضلاع المحدد بالمتجهات U , V:
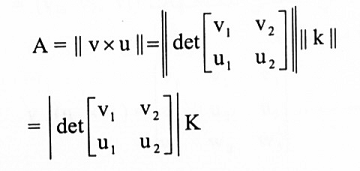
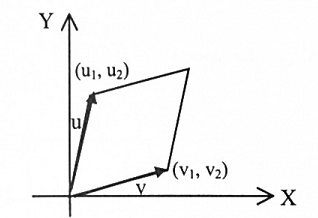
شكل (1-5)
(2) قاعدة متوازي المستطيلات المتكونة من المتجهات W , U, V عبارة عن متوازي الأضلاع المتكونة بواسطة w , u (شكل 1-6).
عليه وبموجب مبرهنة (1-4) فإن مساحة القاعدة هي ||u x w||، وارتفاع متوازي المستطيلات h هو طول المسقط العمودي للمتجه v على u x w.
لذا بموجب الصيغة (9) في (الضرب النقطي , المساقط)

شكل (1-6)
عليه فحجم متوازي المستطيلات:
V = القاعدة × الارتفاع
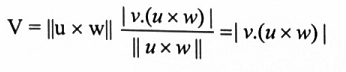
وبموجب الصيغة (5)
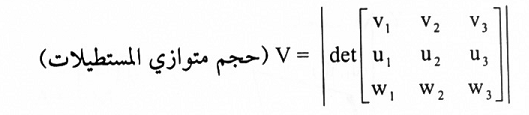
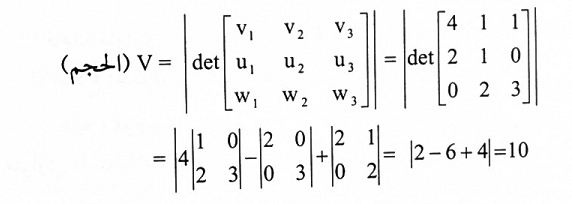
مثال(6): أوجد حجم متوازي المستطيلات المحدد بالمتجهات v = (4,1,1) و u = (2,1,0) و w = (0,2,3) الحل:
تعريف (1-6):
المستويين 1 πو π2 متوازيين إذا كان حاصل ضربهما الاتجاهي يساوي صفراً (π1 x π2 = 0)
مثال (7):
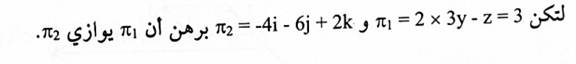
الحل:
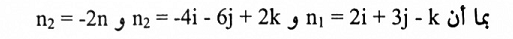
وكذلك n1xn2=0 فإن المستويان متوازيين لاحظ الشكل (1-7)
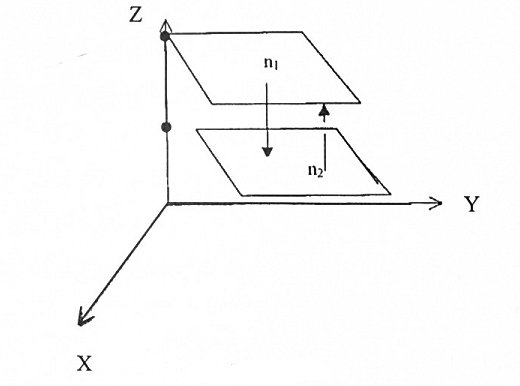
شكل (1-7)
 الاكثر قراءة في الجبر الخطي
الاكثر قراءة في الجبر الخطي
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















