الضرب النقطي ؛المساقط:

يتضمن هذا البند مناقشة طريقة ضرب المتجهات في الفضاء 2- والفضاء 3- مع إعطاء بعض الأمثلة لهذا الضرب هندسياً.

تعريف (1-1):

إذا كانت u , v متجهات مرسومة في الفضاء 2- أو الفضاء 3- بحيث تكون نقاط بدايتهما متطابقة و ⍉ هي الزاوية المحصورة بينهما، فإن الضرب النقطي (أو الضرب الداخلي الإقليدي)، يكتب v.u ويعرف كما يلي:

وإذا كانت v = 0 او u=0 فأن    v.u=0

مثال(1):

نفرض v = (0,2,2) و u = (0,0,1) و ⍉=60

[شكل (1-1)] فإن:

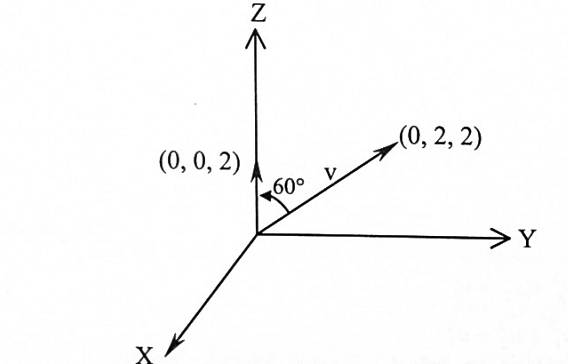
                                                شكل (1-1)

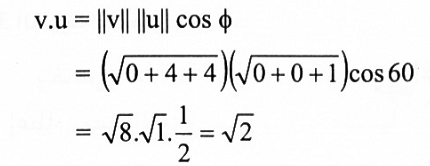
لتكن v = (v₁ , v₂ , v₃) و  u = (u₁ , u₂ , u₃)متجهات غير صفرية و ⍉الزاوية بينهما كما موضح في الشكل (1-2) فإن:

من قانون جيوب التمام نحصل على:

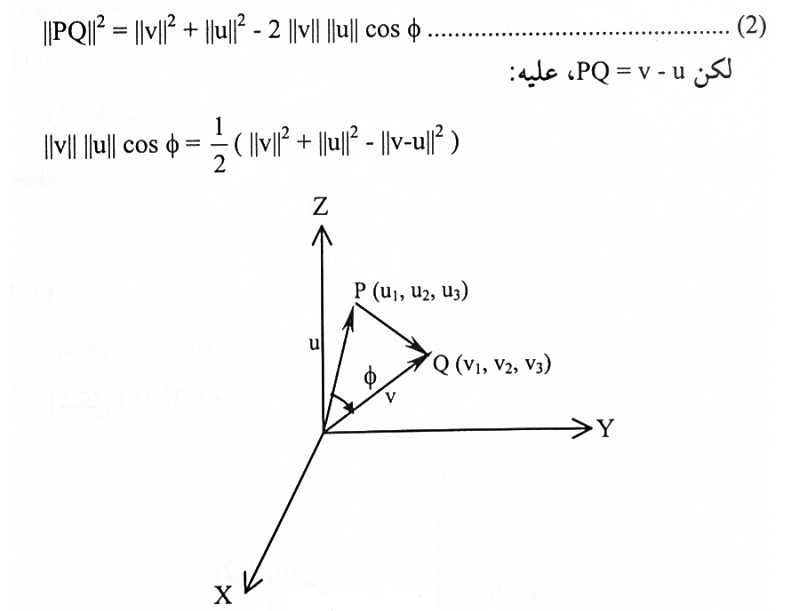
                                                                 شكل (1-2)

وبالتعويض عن :

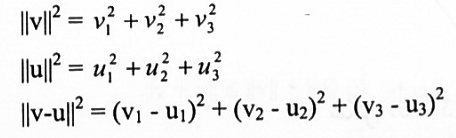
مثال(2):

لتكن u , v متجهات كما في مثال (1). أوجد الزاوية المحصورة بينهما.

الحل:

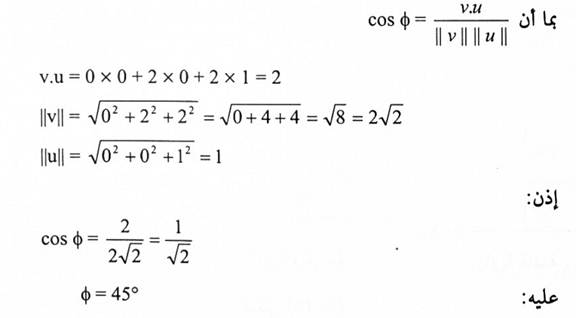
مبرهنة (1-2):

لتكن u , v متجهات مرسومة في فضاء 2- أو فضاء 3- فإن:

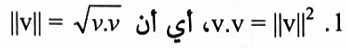
2. لتكن u , v متجهات غير صفرية و ⍉ زاوية محصورة بينهما فإ:

a. ⍉ زاوية حادة إذا وفقط إذا v.u>0

b. ⍉ زاوية منفرجة إذا وفقط إذا v.u<0

c. ⍉ زاوية قائمة (⍉=π/2).إذا وفقط إذا v. u = 0

البرهان:

(1) بما أن الزاوية بين v , v هي صفر فإن:

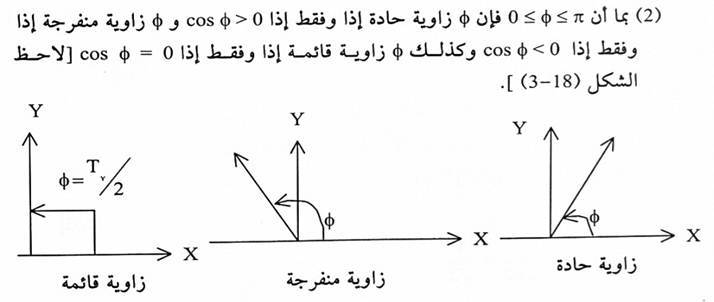
                                                          شكل (1-3)

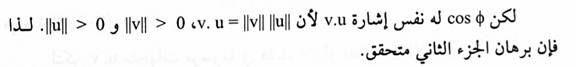
مثال(3):

نفرض v = (2, -3, 4) ، u = (-4 , 3, 1) ، w = (2 , 4, 2) فإن:

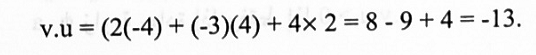
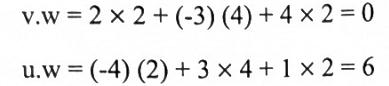
لهذا فإن الزاوية بين u , v منفرجة ، الزاوية بين v و w قائمة. والزاوية بين w , u حادة.

المتجهين u , v يقال لهما بأنهما متعامدين إذا وفقط إذا v . u = 0 يرمز لتعامد u , v بالرمز .u ⟘v

مثال(4):

المتجه غير الصفري n = (a , b) المرسوم في فضاء 2-  يكون عمودياً على المستقيم         ax + by + c = 0.

الحل:

نفرض P₁(x₁ , y₁) ، P₂ ( x₂ , y₂)

نقاط واقعة على المستقيم [ الشكل (1-4)].

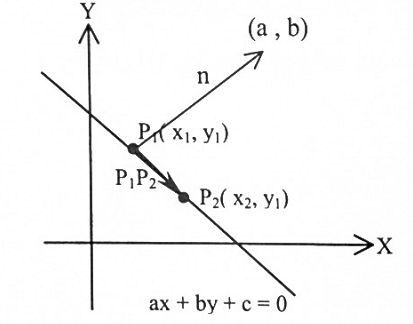
                                      الشكل (1-4)

إذن:

إذن n والمتجه p₁p₂ متعامدين.

مبرهنة (1-3):

لتطن w , u , v متجهات مرسومة في فضاء 2- أو فضاء 3- و k كمية ثابتة، فإن الخواص الآتية تكون صحيحة:

1. v.u = u.v .

2.v . (u + w) = v.u + v.w

3 K (v.u) = (kv) . u = v. (ku).

4. v.v>0 إذا كان v ≠ 0 و v = 0.v  إذا v = 0

البرهان:

نبرهن (1)

نفرض  v = (v₁ , v₂, v₃) و u = (u₁, u₂, u₃)

مثال(5):

لتكن v = (2,0,-3) و u = (6,1,4) فإن:

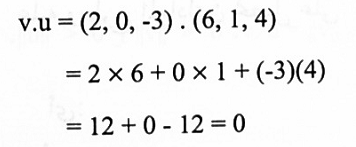
إذنv.u  = 0

عليه فإن v⟘u

المساقط المتعامدة: في بعض التطبيقات نحتاج إلى تحليل المتجه v إلى مركبتين، أحدهما توزي متجه ما مثل a والأخرى عمودية عليه. فإذا فرضنا أن بداية المتجه v تنطبق على بداية المتجه a كما في المثال (5) يمكننا تحليل v بإسقاط عمود من نهايته على المتجه a أو امتداد فنحص على المركبة الأول u₁ والمركبة الثانية ستكون.

u₂=v-u₁                                                                                                                                                                      

U₁ يسمى المسقط العمودي للمتجه v على

A ويرمز له بالرمز Proj_aV، وتسمى

U₂ مركبة المتجه v العمودية على

A وتكتب:                                                      

U₂ = v - proj_aV

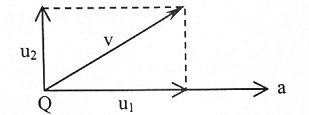
                               شكل ((1-5

ملاحظة:

من الشكل (1-5)، المتجه u₁ موازياً إلى a و u₂ عمودياً على a وأن

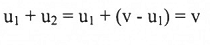
مبرهنة (1-4):

لتكن v و a متجهات مرسومة في فضاء 2- وفضاء 3- وأن a ≠ 0، فإن مركبة المتجه v على امتداد a هي : proj_aV

ومركبة المتجه v العمودية على a هي :

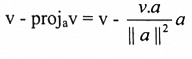
البرهان:

نفرض أن u₁ = proj_aV  ،  u₂ = v - proj_a^v

ويأخذ الضرب النقطي لكلا الطرفين مع المتجه a باستخدام كل من المبرهنتين (1-2) و (1-3) نحصل على:

مثال(6):

لتكن (-3,2) a = و u = (2,1). اوجد مركبة u على امتداد a ومركبته العمودية على a.

ولكي نتحقق من أن u = proj_au عمود على. a

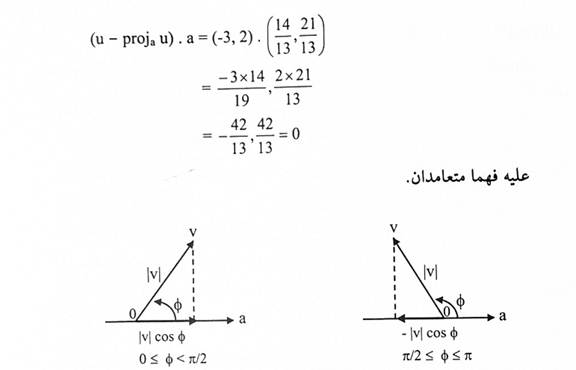
                                                           شكل (1-6)

الزاوية بين مركبة v باتجاه v و a:

المساقط بين نقطة معلومة ومستقيم معلوم:

نفرض P (x₀ , y₀) نقطة معلومة والمستقيم المعلوم ax + by + c = 0 ولتكن Q (x₁, x₂) نقطة على المستقيم. نرسم المتجه (الناظم) n = (a , b) بحيث تكون Q بدايته.

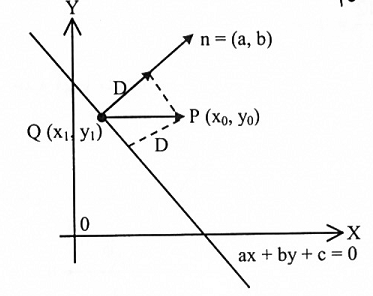
                                                شكل (1-7)

عليه فإن n عمود على المستقيم ، من الشكل (1-7) نلاحظ أن:

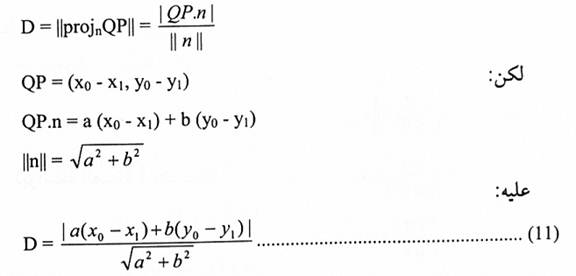
وبما أن النقطة Q تقع على المستقيم فإن مركباتها تحقق معادلة المستقيم.

لذا فإن:                                                           ax₁ + by₁ + c = 0

أي:                                                                         c = -ax₁ - by

وبالتعويض في العلاقة (11) نحصل على:

مثال(7):

          أوجد المسافة من النقطة (-3 , 1) إلى المستقيم 4x + 3y + 4 = 0

الحل:

بالتعويض في العلاقة (12):

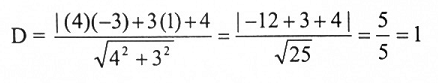
مثال(8): اوجد المسافة بين المستوى 2x – y + 3z = 6 والنقطة Q (3, 5, 7)

الحل:

نعين نقطة على المستوى ولتكن P (3,0,0) (لأنها تحقق المعادلة أعلاه).

الناظم n = (2, -1 , 3)

لهذا PQ = (0 , 5, -7)

 و |PQ. n| = 26 (تحقق من ذلك)

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الشعائر يواصل تحضيراته لتنظيم عمل المواكب الحسينية في زيارة الأربعين

قسم شؤون المعارف يناقش تحضيرات المؤتمر العلمي الأول لمركز تراث البصرة

قسم الشؤون الفكرية يقيم دورة تطويرية لملاكات هيأة المساءلة والعدالة في الأرشفة الإلكترونية

المجمع العلمي ينظم مجلس عزاء في قضاء الهندية

المزيد

الآخبار الصحية

نصائح عملية للحد من التعرق المفرط في الصيف

أطباء يحذرون: مكمل غذائي شائع قد يدمر الجهاز العصبي

تحذير طبي من تأثير جانبي "غير متوقع" لحقن التخسيس

حمامات الثلج قد تكون خطيرة وأحيانا مميتة.. ما السبب؟

المزيد

الآخبار التكنلوجية

أكبر جدارية شمسية في العالم تدخل موسوعة غينيس.. مشروع ضخم

تسارع دوران الأرض يثير القلق.. وتحذيرات من "كوارث محتملة" ؟

"سوذبيز" تطرح أكبر قطعة من المريخ على الأرض في مزاد علني

أوبن أيه آي تعتزم إطلاق متصفح إنترنت يعمل بالذكاء الاصطناعي

المزيد

مواضيع ذات صلة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-تمارين محلولة

فضاء المتجهات الإقليدي-الفضاء الاقليدي النوني

فضاء المتجهات العام- فضاء المتجهات الحقيقي

فضاء المتجهات العام-رتبة المصفوفات بعد الفضاء الصفري

فضاء المتجهات العام-فضاء الصفوف وفضاء الأعمدة والفضاء الصفري

فضاء المتجهات العام- الأساس والبعد

فضاء المتجهات العام-الفضاءات الجزئية

فضاء الضرب الداخلي-الأساسات المتعامدة طريقة كرام ــ شمت

فضاء الضرب الداخلي-الضرب الداخلي

فضاء الضرب الداخلي-المصفوفات المتعامدة، تبديل الأساسات

فضاء الضرب الداخلي-الزوايا والتعامد في فضاء الضرب الداخلي