At a young age we make an unsteady entrance into numberland. We learn that 1 is first in the ‘number alphabet’, and that it introduces the counting numbers 1, 2, 3, 4, 5,. . . Counting numbers are just that: they count real things – apples, oranges, bananas, pears. It is only later that we can count the number of apples in a box when there are none.

Even the early Greeks, who advanced science and mathematics by quantum leaps, and the Romans, renowned for their feats of engineering, lacked an effective way of dealing with the number of apples in an empty box. They failed to give ‘nothing’ a name. The Romans had their ways of combining I, V, X, L, C, D and M but where was 0? They did not count ‘nothing’.

How did zero become accepted?

The use of a symbol designating ‘nothingness’ is thought to have originated thousands of years ago. The Maya civilization in what is now Mexico used zero in various forms. A little later, the astronomer Claudius Ptolemy, influenced by the Babylonians, used a symbol akin to our modern 0 as a placeholder in his number system. As a placeholder, zero could be used to distinguish between examples (in modern notation) such as 75 and 705, instead of relying on context as the Babylonians had done. This might be compared with the introduction of the ‘comma’ into language – both help with reading the right meaning. But, just as the comma comes with a set of rules for its use – there have to be rules for using zero.

The seventh-century Indian mathematician Brahmagupta treated zero as a ‘number’, not merely as a placeholder, and set out rules for dealing with it. These included ‘the sum of a positive number and zero is positive’ and ‘the sum of zero and zero is zero’. In thinking of zero as a number rather than a placeholder, he was quite advanced. The Hindu-Arabic numbering system which included zero in this way was promulgated in the West by Leonardo of Pisa – Fibonacci – in his Liber Abaci (The Book of Counting) first published in 1202. Brought up in North Africa and schooled in the Hindu-Arabian arithmetic, he recognized the power of using the extra sign 0 combined with the Hindu symbols 1, 2, 3, 4, 5, 6, 7, 8 and 9.

The launch of zero into the number system posed a problem which Brahmagupta had briefly addressed: how was this ‘interloper’ to be treated? He had made a start but his nostrums were vague. How could zero be integrated into the existing system of arithmetic in a more precise way? Some adjustments were straightforward. When it came to addition and multiplication, 0 fitted in neatly, but the operations of subtraction and division did not sit easily with the ‘foreigner’. Meanings were needed to ensure that 0 harmonized with the rest of accepted arithmetic.

How does zero work?

Adding and multiplying with zero is straightforward and uncontentious – you can add 0 to 10 to get a hundred – but we shall amean ‘add’ in the less imaginative way of the numerical operation. Adding 0 to a number leaves that number unchanged while multiplying 0 by any number always gives 0 as the answer. For example, we have 7 + 0 = 7 and 7 × 0 = 0. Subtraction is a simple operation but can lead to negatives, 7 − 0 = 7 and 0 − 7 = − 7, while division involving zero raises difficulties.

Let’s imagine a length to be measured with a measuring rod. Suppose the measuring rod is actually 7 units in length. We are interested in how many measuring rods we can lie along our given length. If the length to be measured is actually 28 units the answer is 28 divided by 7 or in symbols 2 8 ÷ 7 = 4. A better notation to express this division is

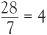
and then we can ‘cross-multiply’ to write this in terms of multiplication, as 2 8 = 7 × 4. What now can be made of 0 divided by 7? To help suggest an answer in this case let us call the answer a so that

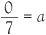
By cross-multiplication this is equivalent to 0 = 7 × a. If this is the case, the only possible value for a is 0 itself because if the multiplication of two numbers gives 0, one of them must be 0. Clearly it is not 7 so a must be a zero.

This is not the main difficulty with zero. The danger point is division by 0. If we attempt to treat 7/0 in the same way as we did with 0/7, we would have the equation

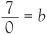
By cross-multiplication, 0 × b = 7 and we wind up with the nonsense that 0 = 7. By admitting the possibility of 7/0 being a number we have the potential for numerical mayhem on a grand scale. The way out of this is to say that 7/0 is undefined. It is not permissible to get any sense from the operation of dividing 7 (or any other nonzero number) by 0 and so we simply do not allow this operation to take place. In a similar way it is not permissible to place a comma in the mid,dle of a word without descending into nonsense.

The 12th-century Indian mathematician Bhaskara, following in the footsteps of Brahmagupta, considered division by 0 and suggested that a number divided by 0 was infinite. This is reasonable because if we divide a number by a very small number the answer is very large. For example, 7 divided by a tenth is 70, and by a hundredth is 700. By making the denominator number smaller and smaller the answer we get is larger and larger. In the ultimate smallness, 0 itself, the answer should be infinity. By adopting this form of reasoning, we are put in the position of explaining an even more bizarre concept – that is, infinity. Wrestling with infinity does not help; infinity (with its standard notation ∞) does not conform to the usual rules of arithmetic and is not a number in the usual sense.

If 7/0 presented a problem, what can be done with the even more bizarre 0/0? If 0/0 = c, by cross-multiplication, we arrive at the equation 0 = 0 ×c and the fact that 0 = 0. This is not particularly illuminating but it is not nonsense either. In fact, c can be any number and we do not arrive at an impossibility. We reach the conclusion that 0/0 can be anything; in polite mathematical circles it is called ‘indeterminate’.

All in all, when we consider dividing by zero we arrive at the conclusion that it is best to exclude the operation from the way we do calculations. Arithmetic can be conducted quite happily without it.

What use is zero?

We simply could not do without 0. The progress of science has depended on it. We talk about zero degrees longitude, zero degrees on the temperature scale, and likewise zero energy, and zero gravity. It has entered the non-scientific language with such ideas as the zero-hour and zero-tolerance.

All about nothing

The sum of zero and a positive number is positive

The sum of zero and a negative number is negative

The sum of a positive and a negative is their difference; or, if they are equal, zero

Zero divided by a negative or positive number is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator

Brahmagupta, AD628

Greater use could be made of it though. If you step off the 5th Ave sidewalk in New York City and into the Empire State Building, you are in the magnificent entrance lobby on Floor Number 1. This makes use of the ability of numbers to order, 1 for ‘first’, 2 for ‘second’ and so on, up to 102 for ‘a hundred and second.’ In Europe they do have a Floor 0 but there is a reluctance to call it that.

Mathematics could not function without zero. It is in the kernel of mathematical concepts which make the number system, algebra, and geometry go round. On the number line 0 is the number that separates the positive numbers from the negatives and thus occupies a privileged position. In the decimal system, zero serves as a place holder which enables us to use both huge numbers and microscopic figures.

Over the course of hundreds of years zero has become accepted and utilized, becoming one of the greatest inventions of man. The 19th-century American mathematician G.B. Halsted adapted Shakespeare’s Midsummer Night’s Dream to write of it as the engine of progress that gives ‘to airy nothing, not merely a local habitation and a name, a picture, a symbol, but helpful power, is the characteristic of the Hindu race from whence it sprang’.

When 0 was introduced it must have been thought odd, but mathematicians have a habit of fastening onto strange concepts which are proved useful much later. The modern day equivalent occurs in set theory where the concept of a set is a collection of elements. In this theory Φ designates the set without any elements at all, the so-called ‘empty set’. Now that is an odd idea, but like 0 it is indispensible.

the condensed idea

Nothing is quite something