

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Squares and square roots
المؤلف:
Tony Crilly
المصدر:
50 mathematical ideas you really need to know
الجزء والصفحة:
23-28
27-2-2016
2537
If you like making squares with dots, your thought patterns are similar to those of the Pythagoreans. This activity was prized by the fraternity who followed their leader Pythagoras, a man best remembered for ‘that theorem’. He was born on the Greek island of Samos and his secret religious society thrived in southern Italy. Pythagoreans believed mathematics was the key to the nature of the universe.

Counting up the dots, we see the first ‘square’ on the left is made from one dot. To the Pythagoreans 1 was the most important number, imbued with spiritual existence. So we’ve made a good start. Continuing to count up the dots of the subsequent squares gives us the ‘square’ numbers, 1, 4, 9, 16, 25, 36, 49, 64,… These are called ‘perfect’ squares. You can compute a square number by adding the dots on the shape ⌉ outside the previous one, for example 9 + 7 = 16. The Pythagoreans didn’t stop with squares. They considered other shapes, such as triangles, pentagons (the figure with five sides) and other polygonal (many-sided) shapes.

The triangular numbers resemble a pile of stones. Counting these dots gives us 1, 3, 6, 10, 15, 21, 28, 36, … If you want to compute a triangular number you can use the previous one and add the number of dots in the last row. What is the triangular number which comes after 10, for instance? It will have 5 dots in the last row so we just add 10 + 5 = 15.
If you compare the square and triangular numbers you will see that the number 36 appears in both lists. But there is a more striking link. If you take successive triangular numbers and add them together, what do you get? Let’s try it and put the results in a table.
Adding two successive triangular numbers
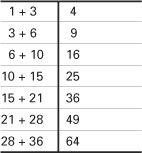
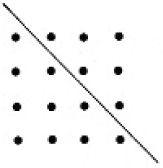
That’s right! When you add two successive triangular numbers together you get a square number. You can also see this with a ‘proof without words’. Consider a square made up of 4 rows of 4 dots with a diagonal line drawn through it. The dots above the line (shown) form a triangular number and below the line is the next triangular number. This observation holds for any sized square. It’s a short step from these ‘dotty diagrams’ to measuring areas. The area of a square whose side is 4 is 4 × 4 = 42 = 16 square units. In general, if the side is called x then the area will be x2.
The square x2 is the basis for the parabolic shape. This is the shape you find in satellite receiver dishes or the reflector mirrors of car headlights. A parabola has a focus point. In a receiving dish a sensor placed at the focus receives the reflected signals when parallel beams from space hit the curved dish and bounce towards the focus point.
In a car headlight a light bulb at the focus sends out a parallel beam of light. In sport, shot-putters, javelin throwers and hammer throwers will all recognize the parabola as the shape of the curved path that every object follows as it falls to the Earth.
Square roots
If we turn the question around and want to find the length of a square which has a given area 16, the answer is plainly 4. The square root of 16 is 4 and written as 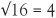 . The symbol √ for square roots has been employed since the 1500s. All the square numbers have nice whole numbers as square roots. For example,
. The symbol √ for square roots has been employed since the 1500s. All the square numbers have nice whole numbers as square roots. For example, 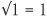 ,
, 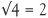 ,
, 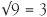 ,
, 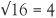 ,
, 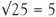 , and so on. There are though many gaps along the numbers line between these perfect squares. These are 2, 3, 5, 6, 7, 8, 10, 11, …
, and so on. There are though many gaps along the numbers line between these perfect squares. These are 2, 3, 5, 6, 7, 8, 10, 11, …

There is a brilliant piece of alternative notation for square roots. Just as x2 denotes a square number, we can write a square root number as x½, which fits in with the device of multiplying numbers together by adding powers. This is the basis for logarithms, invented after we learnt in around 1600 that a problem in multiplication could be changed into one of addition. But that is another story. These numbers all have square roots, but they are not equal to whole numbers. Virtually all calculators have a √ button, and using it we find, for instance, 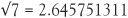 .
.
Let’s look at 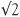 . The number 2 had special significance for the Pythagoreans because it is the first even number (the Greeks thought of the even numbers as feminine and the odd ones as masculine – and the small numbers had distinct personalities). If you work out
. The number 2 had special significance for the Pythagoreans because it is the first even number (the Greeks thought of the even numbers as feminine and the odd ones as masculine – and the small numbers had distinct personalities). If you work out 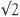 on your calculator you will get 1.414213562 assuming your calculator gives this many decimal places. Is this the square root of 2? To check we make the calculation 1.414213562 × 1.414213562. This turns out to be 1.999999999. This is not quite 2 for 1.414213562 is only an approximation for the square root of 2.
on your calculator you will get 1.414213562 assuming your calculator gives this many decimal places. Is this the square root of 2? To check we make the calculation 1.414213562 × 1.414213562. This turns out to be 1.999999999. This is not quite 2 for 1.414213562 is only an approximation for the square root of 2.
What is perhaps remarkable is that all we will ever get is an approximation! The decimal expansion of  to millions of decimal places will only ever be an approximation. The number
to millions of decimal places will only ever be an approximation. The number 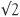 is important in mathematics, perhaps not quite as illustrious as π or e but important enough to gets its own name – it is sometimes called the ‘Pythagorean number’.
is important in mathematics, perhaps not quite as illustrious as π or e but important enough to gets its own name – it is sometimes called the ‘Pythagorean number’.
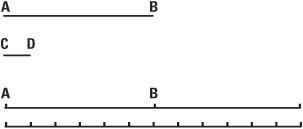
Are square roots fractions?
Asking whether square roots are fractions is linked to the theory of measurement as known to the ancient Greeks. Suppose we have a line AB whose length we wish to measure, and an indivisible ‘unit’ CD with which to measure it. To make the measurement we place the unit CD sequentially against AB. If we place the unit down m times and the end of the last unit fits flush with the end of AB (at the point B) then the length of AB will simply be m. If not we can place a copy of AB next to the original and carry on measuring with the unit (see figure). The Greeks believed that at some point using n copies of AB and m units, the unit would fit flush with the end-point of the mth AB. The length of AB would then be m/n. For example if 3 copies of AB are laid side by side and 29 units fit alongside, the length of AB would be 29/3.

The Greeks also considered how to measure the length of the side AB (the hypotenuse) of a triangle where both of the other sides are one ‘unit’ long. By Pythagoras’s theorem the length of AB could be written symbolically as 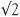 so the question is whether
so the question is whether 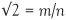 ?
?
From our calculator, we have already seen that the decimal expression for 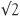 is potentially infinite, and this fact (that there is no end to the decimal expression) perhaps indicates that
is potentially infinite, and this fact (that there is no end to the decimal expression) perhaps indicates that 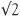 is not a fraction. But there is no end to the decimal 0.3333333… and that represents the fraction ⅓. We need more convincing arguments.
is not a fraction. But there is no end to the decimal 0.3333333… and that represents the fraction ⅓. We need more convincing arguments.
Is 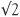 a fraction?
a fraction?
This brings us to one of the most famous proofs in mathematics. It follows the lines of the type of proof which the Greeks loved: the method of reductio ad absurdum. Firstly it is assumed that 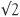 cannot be a fraction and ‘not a fraction’ at the same time. This is the law of logic called the ‘excluded middle’. There is no middle way in this logic. So what the Greeks did was ingenious. They assumed that it was a fraction and, by strict logic at every step, derived a contradiction, an ‘absurdity’. So let’s do it. Suppose We can assume a bit more too.
cannot be a fraction and ‘not a fraction’ at the same time. This is the law of logic called the ‘excluded middle’. There is no middle way in this logic. So what the Greeks did was ingenious. They assumed that it was a fraction and, by strict logic at every step, derived a contradiction, an ‘absurdity’. So let’s do it. Suppose We can assume a bit more too.
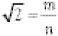
We can assume that m and n have no common factors. This is OK because if they did have common factors these could be cancelled before we began. (For example, the fraction 21/35 is equivalent to the factorless ⅗ on cancellation of the common factor 7.)
We can square both sides of 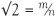 to get 2 = m2/n2 and so m2 = 2n2. Here is where we make our first observation: since m2 is 2 times something it must be an even number. Next m itself cannot be odd (because the square of an odd number is odd) and so m is also an even number.
to get 2 = m2/n2 and so m2 = 2n2. Here is where we make our first observation: since m2 is 2 times something it must be an even number. Next m itself cannot be odd (because the square of an odd number is odd) and so m is also an even number.
So far the logic is impeccable. As m is even it must be twice something which we can write as m = 2k. Squaring both sides of this means that m2 = 4k2. Combining this with the fact that m2 = 2n2 means that 2n2 = 4k2 and on cancellation of 2 we conclude that n2 = 2k2. But we have been here before! And as before we conclude that n2 is even and n itself is even. We have thus deduced by strict logic that both m and n are both even and so they have a factor of 2 in common. This was contrary to our assumption that m and n have no common factors. The conclusion therefore is that 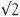 cannot be a fraction.
cannot be a fraction.
It can also be proved that the whole sequence of numbers √n (except where n is a perfect square) cannot be fractions. Numbers which cannot be expressed as fractions are called ‘irrational’ numbers, so we have observed there are an infinite number of irrational numbers.
the condensed idea
The way to irrational numbers

 الاكثر قراءة في هل تعلم
الاكثر قراءة في هل تعلم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















