

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Voting Systems-Preferential Voting: The Hare Method
المؤلف:
W.D. Wallis
المصدر:
Mathematics in the Real World
الجزء والصفحة:
172-175
16-2-2016
1995
We introduced preference lists as a way of representing a voter’s thoughts about the various candidates; they were not actual, physical lists. However, a number of methods have been devised that require a voter to present a preference list. These methods are known collectively as preferential voting or instant runoff voting. Some methods require the voter to list all candidates; others allow a partial list.
The Hare method or alternative vote system was invented by the English lawyer Sir Thomas Hare in 1859. It is most useful in its more general form, for situations where several representatives are to be elected at once . For the moment we look at the simpler version.
The Hare method requires each voter to provide a preference list at the election.
This list is called a ballot. The candidate with the fewest first place votes is eliminated. Then the votes are tabulated again as if there were one fewer candidate, and again the one with the fewest first place votes in this new election is eliminated.
When only two remain, the winner is decided by a majority vote.
Sample Problem 1.1 Suppose there are four candidates for a position, and 24 voters whose preference profile is:
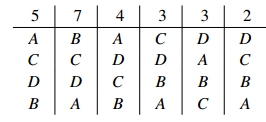
Who would win using the following electoral systems?
(i) The plurality method.
(ii) The runoff method.
(iii) The Hare method.
Solution.
(i) The votes for A, B, C and D are 9, 7, 3 and 5 respectively, so A would win under plurality voting.
(ii) Under the runoff method there is a tie. A and B are retained, and the new preference profile is:

giving 12 votes to each candidate.
(iii) In the Hare method we first eliminate C, who received the fewest first-place votes, obtaining
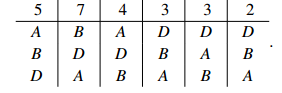
Now we eliminate B:

Your Turn. Repeat the above question for the initial preference profile
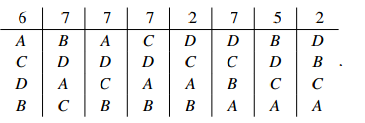
One modification of this method is to allow voters to cast votes only for the candidates of whom they approve. If there are five candidates, and you think A is best, B second, C third, but do not think either D or E is worthy of election, you simply vote A,B,C. If A, B and C are all eliminated, your vote is deleted, and the total number of votes cast is reduced accordingly. We shall refer to these generalized Hare systems as instant runoff systems.
In the above Sample Problem, suppose the seven voters represented by the second column all decided they did not wish to see A or D elected, while those represented by the fifth column did not like C. Then the preference profile is:

Although nine votes is not a majority of the original 24 voters, it may count as a majority for this purpose. In some cases a quota is declared: a number is decided, and if neither of the last two candidates remaining achieves that many votes then the election is declared void. So, if there was a quota of 10 votes, the election would have to be held again.
A complication that can occur in real life is that a voter might not prefer one candidate over another: ties could occur in the voter’s preferences. In practice, electoral systems that use preference lists do not allow ties, so that the voter must make a (possibly arbitrary) choice between the tied candidates. For simplicity, we shall assume that there are no ties in preference profiles.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















