Fractional Fourier Transform
المؤلف:
Ozaktas, H. M.; Zalevsky, Z.; and Kutay, M. A.
المصدر:
The Fractional Fourier Transform, with Applications in Optics and Signal Processing. New York: Wiley, 2000. http://www.ee.bilkent.edu.tr/~haldun/wileybook.html.
الجزء والصفحة:
...
23-12-2021
2666
Fractional Fourier Transform
There are two sorts of transforms known as the fractional Fourier transform.
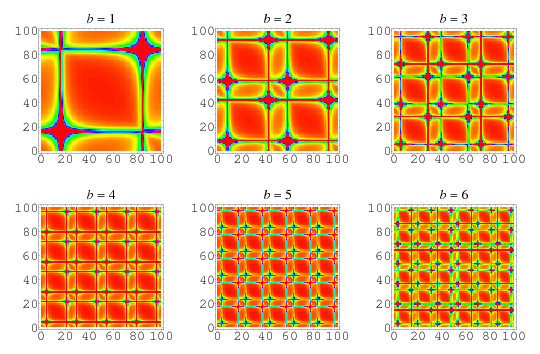
The linear fractional Fourier transform is a discrete Fourier transform in which the exponent is modified by the addition of a factor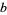 
,
However, such transforms may not be consistent with their inverses unless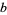 
is an integer relatively prime to 
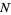so that 
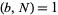. Fractional fourier transforms are implemented in the Wolfram Language as Fourier[list, FourierParameters -> ![<span style=]()
{" src="https://mathworld.wolfram.com/images/equations/FractionalFourierTransform/Inline5.gif" style="height:16px; width:4px" />a, b![<span style=]()
}" src="https://mathworld.wolfram.com/images/equations/FractionalFourierTransform/Inline6.gif" style="height:16px; width:4px" />], where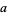 
is an additional scaling parameter. For example, the plots above show 2-dimensional fractional Fourier transforms of the function 
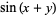for parameter 
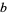ranging from 1 to 6.
The quadratic fractional Fourier transform is defined in signal processing and optics. Here, the fractional powers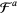 
of the ordinary Fourier transform operation 
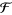correspond to rotation by angles 
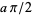in the time-frequency or space-frequency plane (phase space). So-called fractional Fourier domains correspond to oblique axes in the time-frequency plane, and thus the fractional Fourier transform (sometimes abbreviated FRT) is directly related to the Radon transforms of the Wigner distribution and the ambiguity function. Of particular interest from a signal processing perspective is the concept of filtering in fractional Fourier domains. Physically, the transform is intimately related to Fresnel diffraction in wave and beam propagation and to the quantum-mechanical harmonic oscillator.
REFERENCES:
Ozaktas, H. M.; Zalevsky, Z.; and Kutay, M. A. The Fractional Fourier Transform, with Applications in Optics and Signal Processing. New York: Wiley, 2000. http://www.ee.bilkent.edu.tr/~haldun/wileybook.html.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
