Bootstrap Percolation
المؤلف:
Aizenman, M. and Lebowitz, J
المصدر:
Metastability Effects in Bootstrap Percolation." J. Phys. A 21
الجزء والصفحة:
...
21-8-2021
3695
Bootstrap Percolation
A two-dimensional binary (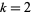
) totalistic cellular automaton with a von Neumann neighborhood of range 
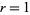. It has a birth rule that at least 2 of its 4 neighbors are alive, and a survival rule that all cells survive. 
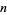steps of bootstrap percolation on an 
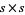grid with random initial condition of density 
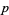can be implemented in the Wolfram Language as
With[{n = 10, p = 0.1, s = 20},
CellularAutomaton[
{1018, {2, {{0, 2, 0}, {2, 1, 2}, {0, 2, 0}}},
{1, 1}},
Table[If[Random[Real] < p, 1, 0], {s}, {s}],
n
]
]
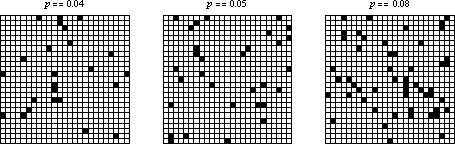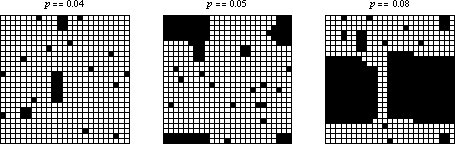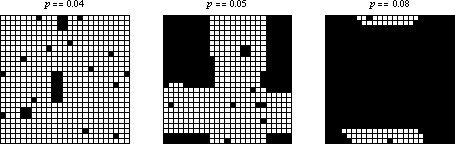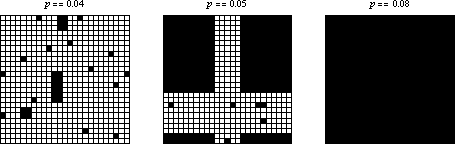
If the initial condition consists of a random sparse arrangement of cells with density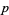 
, then the system seems to quickly converge to a steady state of rectangular islands of live cells surrounded by a sea of dead cells. However, as 
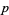crosses some threshold on finite-sized grids, the behavior appears to change so that every cell becomes live. Several examples are shown above on three 
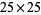grids with random initial conditions and different starting densities.
However, this conclusion proves to be incorrect, since the apparent change in behavior actually is a spurious edge effect introduced by use of a finite-sized grid. Amazingly, Holroyd (2003) showed that the asymptotic threshold occurs such that
REFERENCES:
Aizenman, M. and Lebowitz, J. "Metastability Effects in Bootstrap Percolation." J. Phys. A 21, 3801-3813, 1988.
Gray, L. "A Mathematician Looks at Wolfram's New Kind of Science." Not. Amer. Math. Soc. 50, 200-211, 2003.
Holroyd, A. "Sharp Metastability Threshold for Two-Dimensional Bootstrap Percolation." Prob. Th. and Related Fields 125, 195-224, 2003.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 337-342, 2002.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
