In 1852, William Rowan Hamilton wrote to Augustus de Morgan concerning a problem that had been posed by a student, Frederick Guthrie. Guthrie said:

cartographers know that any map (our definition) can be colored using four or less colors; is there a mathematical proof? (Guthrie later pointed out that the question had come from his brother, Francis Guthrie.)

Kempe published a purported proof in 1879. It was thought that the matter was over, but in 1890 Heawood pointed out a fallacy in Kempe’s proof. Heawood did however repair the proof sufficiently to prove that every planar map can be colored in five colors.

After Heawood’s paper appeared, there was renewed interest in what became known as the four-color problem. Because it was easy to state and tantalizingly difficult to prove, it became one of the most celebrated unsolved problems in mathematics. In 1976, Appel and Haken finally proved that any map can be colored in at most four colors. Their proof involved computer analysis of a large number of cases, so many that human analysis of all the cases is not feasible. So we have Theorem 3 (The Four-Color Theorem). Every map can be colored using at most four colors.

We define a coloring (or vertex-coloring) of a graph to be a way of applying a set of labels, called colors, to the vertices. The coloring is called proper or correct if no two vertices that receive the same color are neighbors. So instead of coloring a map we could instead apply the colors to the vertices of the corresponding graph. The result is to divide the set of vertices into disjoint subsets, where each subset consists of the vertices that receive a specific color. The subsets are called color classes. A proper coloring of G is a coloring in which no two adjacent vertices belong to the same color class. In symbols, if ξ(x) denotes the color assigned to vertex x, then

                                       x ∼ y ⇒ ξ(x) = ξ(y).

A proper coloring is called an n-coloring if it uses n colors; if G has an n-coloring,  then G is called n-colorable. So the Four-Color Theorem says that every planar graph is four-colorable.

The chromatic number χ(G) of a graph G is the smallest integer n such that G has an n-coloring. A coloring of G in χ(G) colors is called minimal. We use the phrase  “G is n-chromatic” to mean that χ(G) = n (but note that a minority of authors use n-chromatic as a synonym for n-colorable).

Incidentally, ξ and χ are the Greek letters “xi” and “chi.” In Greek words, ξ is pronounced like ks in English, while χ has a ch sound.

A cycle of length v has chromatic number 2 if v is even and 3 if v is odd. The star K1,n has chromatic number 2. Clearly χ(G) = 1 if G has no edges and χ(G) ≥ 2 if G has at least one edge. The complete graph on n vertices has chromatic number n.

There are two useful results when looking for chromatic numbers. The first is that, if the graph G has a subgraph H, then χ(G) cannot be smaller than χ(H).

The second, known as Brooks’ Theorem, says that if G is any graph other than a complete graph or a cycle of odd length, then the chromatic number of a graph G is never greater than the maximum degree in G; however, it can be less.

There is no good algorithm to color a graph in the minimum number of colors.

One method, sequential coloring, proceeds as follows. First, list the vertices in some order. (The usual method is to arrange the vertices in order of increasing degree.)

Apply color 1 to the first vertex in the list. Delete that vertex and all its neighbors,  and apply color 1 to the first remaining vertex. Again, delete that vertex and all its neighbors. Continue until the list is empty. Then delete all vertices that received color 1, and apply the same technique to the new list, using color 2. And so on.

The sequential coloring method usually gives a good result, but not necessarily a minimal coloring. For example, consider the 6- cycle abcde f . It can be colored in two colors  (with color classes {ace} and {bd f }), but if the vertices are listed as a,d,c, f,b,e three colors will be needed.

If you want to find a minimal coloring of a relatively small graph, one useful technique is to find the largest complete subgraph in the graph, and color its vertices with different colors. It is then often possible to color the other vertices by brute force (that is, try all possibilities). For example, in the graph of Fig. 1.1, the vertices x₁, x₅ and x₆ form a K₃. Start by coloring them with three different colors. It is then easy to see that the whole graph can be colored in three colors. The color classes are:

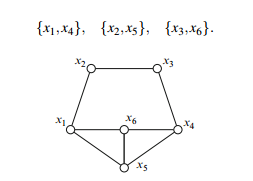
Fig. 1.1 A graph with chromatic number 3

Colorings are often used to avoid conflicts. One example is examination scheduling.

In this case the vertices represent tests, and an edge means some student must take both the tests represented by the endpoints. So we color the graph; tests receiving same color may be run at the same time. Another is the setting up of a habitat zoo. This is a zoo that consists of several large habitats, each containing several species. Obviously one cannot put natural enemies together. So we form a graph whose vertices are species, and an edge means the two species are “enemies.”  Now color this graph, and put species in same habitat if they receive the same color.

The data for a conflict situation is often given in an array. The rows and columns represent the various elements that may conflict (in our examples, the tests and the species). If elements i and j are incompatible, there is a cross in the (i, j) and (j,i)  positions. Replacing crosses by 1s and blanks by 0s produces the incidence matrix of the graph. This information is then used to generate the graph. (Be careful:  sometimes authors find it easier to construct an array in which a cross indicates compatibility.)

Sample Problem 1.1 The following table shows the pairs of species in a habitat zoo that are incompatible.

Find the minimum number of habitats that will be needed.

Solution. For convenience, we have drawn the corresponding graph. We need to color it with the minimum number of colors.

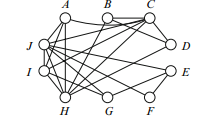
First observe that A, C, H, I, and J are all adjacent to each other; they form a complete graph of size 5. So at least 5 colors are needed. Let’s use 1 for A, 2 for C, 3 for H, 4 for I, and 5 for J.

Now look at B. It is joined to C, D, and H. So colors 2 and 3 are not available.

We shall try color 1 (which is possible because A and B are not joined).

Next consider D. It is joined to B, C, H (and no others). It can take color 4 or 5. We shall try 4.

Finally. a little experimentation shows that E, F and G can take colors 1, 2 and 3 respectively with no problem. This is not the only solution, but it shows that five colors is a possibility. Since at least five are needed, the chromatic number is 5 and at least five habitats are required. In our solution, the habitats are {A,B,E}, {C,F}, {G,H}, {D,I}, and{J},