


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 26-10-2020
التاريخ: 22-5-2016
التاريخ: 2023-10-22
التاريخ: 7-3-2016
|
انكسار الضوء: قانون سنل
عندما تدخل حزمة من الضوء إلى الماء قادمة من الهواء فإن مسارها ينحني كما هو مبين في الشكل 1)). ويسمى التغير في اتجاه الشعاع عند مروره من وسط إلى آخر انكساراً. والزاوية 1θ هي بالطبع زاوية السقوط والزاوية 2θ تسمى زاوية الانكسار. (ينعكس جزء أيضأً من الحزمة من على سطح الماء، كما هو مبين بالشعاع المنقطع في الشكل (1)).

الشكل 1)): عندما يسقط شعاع ضوئي في الهواء على سطح الماء فإن جزءاً من الشعاع يتكسر نحو العمود المقام على السطح. أما الجزء الآخر من الشعاع الساقط فيتبع قانون الانعكاس.
والسبب الأساسي وراء تغير اتجاه الشعاع عند انتقاله من وسط شفاف إلى وسط شفاف آخر أن انتقال الضوء ينتقل بسرعات مختلفة في الأوساط المختلفة. أن للضوء أقصى سرعة C عنما يتحرك في الفراغ وأنه يتحرك أكثر بطئاً في المواد الأخرى. ويوصف المدى الذي يخفض فيه الوسط من سرعة الضوء بما يطلق عليه معامل انكسار الوسط n:
(1) 
الجدول 1)): معاملات الانكسار عند طول موجي مقداره .589 nm

عند معدلي الضغط ودرجة الحرارة.
ومعامل الانكسار أكبر من الواحد دائماً لأن الضوء يسير بأقصى سرعة في الفراغ ويحتوي الجدول 1)) على قيم نموذجية لمعامل الانكسار n، حيث يلاحظ أن معامل الانكسار يقترب من الواحد الصحيح بالنسبة للهواء في حين يكون معامل الانكسار كبيراً بالنسبة للألماس وهو 2.42. ومن الطبيعي أن معامل انكسار الفراغ هو واحد صحيح تماماً ويتغير معامل الانكسار بشكل طفيف بتغير الطول الموجي للضوء كما سنرى فيما بعد وتكون قيمته اكبر للضوء الأزرق بالنسبة للقيمة عند الضوء الأحمر.
من المناسب دراسة حركة الجبهات الموجية لموجة مستوية كما هو مبين في الشكل 2)) لكي نصل إلى علاقة بين زاوية السقوط 1θ وزاوية الانكسار 2θ سنفترض أن سرعة الموجة v1 في الوسط 1 ، و v2 في الوسط 2 بحيث كانت v1 اكبر من v2 وسيكون للجبهات الموجية انحناءة عند السطح للوسطين لأن الموجة تتحرك ببطء أكبر في الوسط 2 عنها في الوسط 1.
افترض أنه يلزم وقت مقداره t لكي تنتقل جبهة الموجة ABC إلى الوضع A'B'C' ولهذا فالمسافة التي تتحركها الجبهة الموجية في الوسط 2 في زمن مقداره t هو b = v2t والمسافة التي تحركها الجبهة الموجية في الوسط 1 هو d = v1t فإذا قسمنا d على b لوجدنا أن:


الشكل 2)): بما أن الموجة تنتقل بشكل أبطأ في الوسط 2 عنها في الوسط 1، فإن المسافة AA' تكون أصغر من المسافة .CC'
وتلاحظ في الشكل بالإضافة إلى ذلك أن:

وإذا قسمنا إحدى المعادلتين على الأخرى نجد أن:

وحيث أن 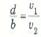 ،إذن
،إذن
(2) 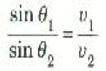
وقد عرفنا من تعريف معامل الانكسار أن v = c/n ولذا يمكننا إعادة كتابة المعادلة (2) كالتالي:

ويمكن إعادة كتابة هذه المعادلة لتصبح
(3) 
وهو ما سنشير إليه بأنه قانون سنل. وهناك طريقة سهلة لتذكر قانون سنل وهي:
عندما يعبر الضوء الحدود بين وسط وآخر حاصل ضرب n sin θ يظل ثابتاً.
وعلينا تذكر أن زاويتي السقوط والانكسار تقاسان دائماً بالنسبة للعمود المقام على الحد الفاصل بين الوسطين.
نستطيع من ملاحظة المعادلة (3) أنه لو كان n2 أكبر من n1، فإن sin θ1 سيكون أكبرsin θ2 مما يعني أن 1θ أكبر من 2θ وهذه هي الحالة المبينة في الشكل (3 أ).إلا أنه قد يحدث أحياناً أن نهتم بالحالة العكسية، حيث n2 أصغر من n1. وهي حالة حزمة ضوئية تنتقل من الزجاج إلى الهواء مثلاً، وفي هذه الحالة فإن المعادلة (3) ستتنبأ لنا بأن 2θ أكبر من 1θ كما هو مبين في الشكل (3 ب).

الشكل 3)): (أ) إذا كان n2 > n1 فإن الشعاع يميل نحو العمود. (ب) إذا كان n2 < n1 فإن العكس هو الصحيح.
إذا كان n2 > n1 فإن الشعاع ينحني نحو العمود ؛ أما إذا كان n2 < n1 فإن الشعاع يبتعد عن العمود.
علينا ملاحظة حالة خاصة مهمة تتعلق بالسقوط العمودي θ1 = 0)) حيث يصبح حل المعادلة (3) في هذه الحالة هو θ2= 0 بغض النظر عن قيم v2 وv1 التي لدينا وعموماً فإن،
لا يغير الضوء الساقط عمودياً على السطح الفاصل بين وسط وآخر من اتجاهه عند دخوله إلى الوسط الثاني.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|