Richard Feynman

In Far Rockaway

“Some facts about my timing: I was born in 1918 in a small town called Far Rockaway, right on the outskirts of New York, near the sea,” begins the first of the monologue books, Surely You’re Joking, Mr. Feynman. “Charmed lives were led by the children of Far Rockaway, a village that amounted to a few hundred acres of frame houses and brick apartment blocks on a spit of beach floating off Long Island's south shore,” writes Feynman's biographer James Gleick. “The neighborhood had been agglomerated into the political entity of New York City as one of the more than sixty towns and neighborhoods that merged as the borough of Queens in 1898.”

The citizens of Far Rockaway worked hard and maintained a respectable middle-class existence. Richard's father, Melville, struggled through the Depression era with a series of entrepreneurial endeavors that never quite met his expectations: sale of a car wax called Whiz, a real estate business, and a chain of dry-cleaning stores. Finally he took a job as a sales manager for a large company that dealt in uniforms.

Melville would have been a scientist if he had had the means. Just before Richard was born he said, “If it's a boy, he'll be a scientist.” (Note that Feynman's sister, Joan, also became a physicist.) Melville had no formal training in science but he had common sense in depth. “In a way, he never knew the facts very well. But he knew truths,” Feynman told another biographer, Jagdish Mehra, and continued, “I find him now, when I look back, a very remarkable man. . . . [He] had a complete understanding of what not to pay attention to, the difference between naming things and the facts, the fact that if you looked into things you always found exciting things. He had a complete understanding of the deeper flavor of science, which he communicated to me.”

Melville was Richard’s first teacher. His principal medium was the Encyclopaedia Britannica, which he read to his son, explaining as they went along. “Everything we read had to be translated into understandable things,” Feynman told Mehra, “and this also became a characteristic of my own and my work all the time. I [still] find great difficulty in understanding most things that other people are doing or how they do them. I always try to translate back, back, back, into some way that I can understand.”

Richard's mother, Lucille, came from a higher economic stratum than Melville. Her father was a successful designer of women's hats, and the family had moved up from a tenement on the Lower East Side to a townhouse uptown on Ninety second Street near Park Avenue. Moving from Park Avenue to Far Rockaway may have been trying for Lucille, but she did not complain. Her defense was a sense of humor, which shaped her son's personality as much as Melville's science lessons. Feynman writes, in another one of his monologue books, What Do You Care? “Although my mother didn't know anything about science, she had a great influence on me as well. In particular, she had a wonderful sense of humor, and I learned from her that the highest forms of understanding we can achieve are laughter and human compassion.” One of Lucille's lines later in her life, when her son was famous and celebrated as the “smartest man in the world”: “If that's the world's smartest man, God help us.”

Richard's main interests in high school were mathematics, science, and girls, perhaps not in that order. He taught himself the rudiments of calculus from the first book on the subject added to the school library, Calculus for the Practical Man. In his senior year in high school, he joined Abram Bader's honors physics course. Bader had studied statistical mechanics and quantum mechanics under Isidor Rabi at Columbia University, but had dropped out of the Ph.D. program when his money ran out. He was a well-informed and sympathetic teacher, and quickly recognized Richard's talent. “Feynman was sui generis,” Bader told Mehra. “In only one day he stood out as the top student in a class of top students.” The top student was bored, however, and Bader gave him Frederick Woods's Advanced Calculus to study. In a month, Richard had read the book, and answered questions Bader had noted in the margins when he had studied the book.

Bader also taught Richard some impressive physics lessons. He emphasized the importance of energy functions. There is, he pointed out, the sum of the function T for kinetic energy and the function V for potential energy. This function, called the “Hamiltonian” (for William Rowan Hamilton, the Irish mathematician and physicist, who based an elaboration of Newton's dynamics on this function), is represented with H,

             H = T + V.          (1)

Equally important is the function L, equal to the difference between T and V,

                 L = T - V,         (2)

and called the “Lagrangian” (for Joseph Lagrange, the eighteenth-century French physicist and mathematician, who based his elaboration of Newton's dynamics on L).

The Hamiltonian function appears in differential equations, which have to be solved (that is, integrated) to define the motion of an object, which is sometimes a difficult task. The Lagrangian function leads to the same result by an entirely different mathematical route. It is integrated with respect to time over any possible path followed by a moving object, to define another function called the “action,” represented with S,

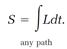                                              (3)

The distinctive thing about the action, called the principle of least action, is that action has its lowest value, a minimum, for the actual path followed by a moving object. Thus the action, constrained so it gives a minimum value, defines that path. For Richard this was a revelation, the awakening of his physical intuition. As he told Mehra, “Instead of differential equations, it tells the property of the whole path. And this fascinated me. That was the greatest thing ever. The rest of my life I have played with action, one way or another, in all my work. I loved it always.”

As for the girls in Richard's adolescent life, there was only one he took seriously. She was the popular and artistic Arline Greenbaum. (Curiously, Feynman, or at any rate his editors, spell her name “Arlene” in the monologue books.) Richard and Arline met when they were both thirteen. “She was a very lovely  and pleasant girl, rather sweet. She had deep dimples, and everybody liked her,” reports one of Richard's former rivals.

Richard graduated from Far Rockaway High School in triumph. He captured most of the honors, and the romance with Arline was forever. University was next. His rejection by Columbia, after a steep application fee, can probably be blamed on a quota for Jewish students. He was accepted at the Massachusetts Institute of Technology (MIT), and arrived in Cambridge in the fall of 1935, in the company of prospective fraternity brothers.

QED and QED

The theory of quantum electrodynamics is “the jewel of physics our proudest possession,” Feynman writes in his fine book for the lay reader, QED. Few would disagree. The theory has been applied to a world of physical effects with complete success. Some of these phenomena permit measurements of astonishing accuracy, and calculations dictated by Feynman's approach to QED are in agreement. For example, the strength of the magnetic field carried by an electron, the electron's “magnetic moment,” has been measured as 1.00115965221 (in certain units), with an uncertainty of about 4 in the last digit. (This number is predicted to be exactly 1 in Dirac’s theory.) The theory calculates 1.00115965246, with an uncertainty of about 20 in the last digits, for the electron's magnetic moment. If you could measure the distance from New York to Los Angeles with this accuracy, you would have it accurate to within the thickness of a human hair.

QED concerns two kinds of elementary particles, electrons and photons, and a multitude of ways they can interact. As usual in quantum mechanics, the theory is limited to statistical calculations. An “amplitude” is calculated for a certain event from which the probability for the event can be determined. There is no way to dig deeper than the probabilities. “There are no ‘wheels and gears’ beneath this analysis of Nature,” Feynman writes. “If you want to understand Her, this is what you have to take.”

The theory does its impressive work by recognizing just three kinds of actions among electrons and photons: Feynman describes them in QED as (1) “a photon goes from point to point”; (2) “an electron goes from point to point”; and (3) “an electron emits or absorbs a photon.” Each action has a certain amplitude. If the two points are A and B, we can follow Feynman in QED and use P(A to B) to represent the amplitude for the first action, and E(A to B) for the second. The amplitude for the third is simply a number whose value is about -0.1 (in certain units), which also equals the electric charge on the electron. Feynman uses j in QED to represent this number.

Thus in a QED calculation Feynman-style for a process, let's say two electrons starting at points 1 and 2 in space and time, and ending at points 3 and 4, as shown in the simple “Feynman diagram” on the left in figure 1.1, we need to know the two amplitudes E(1 to 3) and E(2 to 4).

In a detailed calculation, we would consult a set of rules, called “Feynman Rules,” to find the mathematical form of the two E functions. No photon is involved, so no Ps or js enter the calculation. The amplitude for the process proceeding this way has the form E(1 to 3) × E(2 to 4). This is only one way the electrons can get from points 1 and 2 to points 3 and 4. The diagram on the right in figure 1.1 shows another way whose amplitude calculation has the different form E(1 to 4) × E(2 to 3). Combining (adding or subtracting) the two amplitudes gives a first approximation for the event.

Because the two electrons carry electrical charge, they interact with each other through a force carried by a photon. That possibility is not recognized in the diagrams of figure 1.1. The Feynman diagrams shown in figure 1.2 represent two ways our event can be realized with the interaction mediated by a single photon. An electron first travels from point 1 to point 5. Then it emits a photon, represented by a wavy line, and continues on from point 5 to point 3. A second electron begins at point 2, absorbs the photon at point 6, and continues from point 6 to point 4. Now the calculation must include the amplitudes E(1 to 5), E(5 to 3), E(2 to 6), and E(6 to 4) for the electrons, P(5 to 6) for the photon, and j twice, once for the emission of the photon and again for the absorption. The form of the calculation, read directly from the diagram, is

       E(1 to 5) × j × E(5 to 3) × P(5 to 6) × E(2 to 6) × j × E(6 to 4).

For a better approximation to the amplitude for our event we add this result to the first two. Notice that j occurs twice in the calculation, as the product j × j = j². Because j is small in magnitude (about equal to 0.1), and the product j² is still smaller (about equal to 0.01), this term compared to the first one makes a minor

Figure 1.1. Feynman diagrams for two ways two electrons can get from points 1 and 2 in space and time to points 3 and 4.

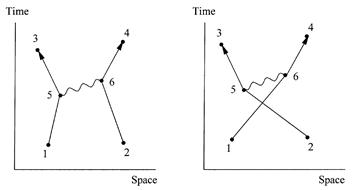
Figure 1.2. Feynman diagrams for two more ways two electrons can get from points 1 and 2 in space and time to points 3 and 4. These paths involve interaction between the electrons mediated by a photon.

contribution to the total amplitude for the event. The Feynman diagram on the right in figure 1.2 shows another way the event can occur with a photon mediating the interaction. The photon that appears in these diagrams as a wavy line represents an electromagnetic interaction between the two electrons, but it has only a transient existence. It is not an ordinary photon that can travel great distances. It exists only for the very short time the uncertainty principle allows it to. In the parlance of particle physics, it is a “virtual photon.”

The Feynman calculation is an open-ended affair. We can go on drawing Feynman diagrams and formulating the corresponding calculations ad infinitum. Figure 1.3 depicts one more possibility for the two-electron event we have been considering. Here two photons are involved and both electrons emit and absorb a photon. The calculation now includes four j factors, that is, the product j ⁴, which is equal to about 0.0001, and its contribution to the total amplitude for the event is even smaller compared to those already considered. Fortunately for those who pursue calculations of this kind, the pattern we are seeing is a general one. As the Feynman diagrams proliferate and get more complicated, the calculations they dictate get less important and more expendable.

This account has so far omitted a major aspect of electron behavior, spin, and

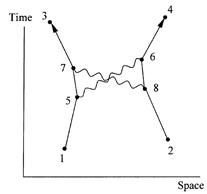
Figure 1.3. Feynman diagram for still another way two electrons can get from points 1 and 2 to points 3 and 4. Each electron emits and absorbs a photon.

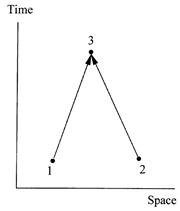
Figure 1.4. Feynman diagram for two electrons attempting to occupy the same point in space and time. The amplitude for this process is zero if the two electrons have the same spin state, nonzero if they have different spin states.

a powerful principle: two electrons in the same spin state cannot occupy the same point in space and time. Thus the amplitude corresponding to the diagram in figure 1.4, showing two electrons with the same space-time destination, must be equal to zero if the two electrons have the same spin state. This is another way to put the Pauli exclusion principle, which we introduced earlier in the language of quantum numbers. The general idea is that two electrons with the same physical description refuse to come together; in fact, they deliberately avoid each other.

Feynman's diagrams, aided by the exclusion principle, tell much of the story of electrons and photons, and the electromagnetic force that governs their behavior. As Feynman puts it in QED, the theory offers “a terrific cornucopia of variety and excitement that comes from the exclusion principle and the repetition again and again of the three very simple actions P(A to B), E(A to B), and j.”