


 Grammar
Grammar
 Tenses
Tenses
 Present
Present
 Past
Past
 Future
Future
 Parts Of Speech
Parts Of Speech
 Nouns
Nouns
 Verbs
Verbs
 Adverbs
Adverbs
 Adjectives
Adjectives
 Pronouns
Pronouns
 Pre Position
Pre Position
 Preposition by function
Preposition by function 
 Preposition by construction
Preposition by construction
 Conjunctions
Conjunctions
 Interjections
Interjections
 Grammar Rules
Grammar Rules
 Linguistics
Linguistics
 Semantics
Semantics
 Pragmatics
Pragmatics
 Reading Comprehension
Reading Comprehension|
Read More
Date: 2024-02-05
Date: 21-1-2022
Date: 2023-10-10
|
Defining productivity: Quantitative approaches
Proposing a dichotomy between quantitative and qualitative notions of productivity may blur the fact that the two are closely related. Thus the idea of potentiality, which is central to qualitative definitions of productivity, can be expressed in the statistical terms of probability. If something can happen, it should be possible to quantify the probability of its occurrence. This is the essential insight behind Bolinger's definition of productivity as "the statistical readiness with which an element enters into new combinations" (1948:18). Since the formulation of this insight about half a century ago, a number of productivity measures have been proposed.
There is one quantitative definition that is probably the most widely used and the most widely rejected at the same time. This definition says that the productivity of an affix can be measured by counting the number of attested types with that affix at a given point in time. No linguist would seriously advocate this view of productivity as a single measure because it goes against the crucial idea of productivity as "a design feature of language" (Bauer 1994:3354). Thus there can be many words with a given affix, but nevertheless speakers will not use the suffix very often to make up new words. As mentioned above, language is a system which speakers can use creatively to produce and understand new words and sentences. Reference to existing, lexicalized words cannot shed any light on this central capacity of language. Nevertheless, in many publications 'productivity' is used with reference to the number of existing words, possibly only for lack of a better term. We will shortly see that, together with other measures, the number of attested derivatives can still be of interest to the morphologist.
Lieber (1980:177ff) suggests that the productivity of an affix should be equated with the number of forms that could potentially be derived with that suffix, which in turn is a function of the number of words that can undergo the process. This definition is problematic because in her own theory there is no place for actual words. Consider, for example, the case of nominalizing -ity, which is extremely productive with bases in -able. In Lieber's framework, however, -ity must be considered to be rather unproductive, because the number of potential base words in -able does not count for the determination of the productivity of -ity because there is only the lexical entry for -able, so that the suffix -able counts as much for the productivity of -ity as any individual base word.
This counterintuitive result is avoided by definitions that make reference to actual words. For example, Aronoff (1976) suggests a productivity index which is the ratio of actual to possible words. The higher this ratio, the higher the productivity of a given rule. Largely ignored by later authors, this measure had already been proposed earlier by Berschin, who labels it "Besetzungsgrad" ('degree of exhaustion', 1971:44-45). Anshen and Aronoff (1981:64) point out the main weakness of this proposal: for extremely productive and for completely unproductive processes it makes wrong predictions. Thus, with highly productive affixes like -ness the number of possible words is, in principle, infinite, which necessarily leads to a comparatively low productivity index. With unproductive rules like -th nominalization it is unclear how the ratio of actual to possible words should be calculated. If one considers all actual words with this suffix as possible words, the ratio equals 1, which is the highest possible score and therefore counterintuitive. If, however, the number of possible words with this suffix is considered zero, the index cannot be computed at all.
Another, more general problem of Lieber's, Berschin's and Aronoffs proposals is how to actually count the number of possible words, since, as we have discussed above, the number of possible formations on the basis of a productive rule is, in principle, uncountable. How can one quantify something that is, in principle, uncountable?
A partial solution to this problem is provided by Baayen (1989, 1992, 1993), who proposes the reverse of Aronoffs productivity index, and calls this the 'potentiality' of a given rule. This potentiality measure I is the quotient of the number of possible forms S and the number of actual forms V with a given affix in a sufficiently large corpus of text. Using certain statistical models, the number of potential forms with a given affix can be estimated on the basis of the grouped frequency distributions of the forms attested in the corpus.1
Although this potentiality measure seems to capture an important property of morphological rules, it has the serious drawback that all truly productive processes should have infinite S. This is, however, not the case. For example, Baayen (1992:121) finds that some productive processes (e.g. agentive -er and diminutive -tje in Dutch) have infinite values of S, whereas other productive processes (such as the Dutch abstract noun forming suffixes -sel or -heid) have finite values. From these results Baayen concludes that I should be regarded not as a measure of productivity as such but as a measure of the degree of exhaustion of a productive process and emphasizes the fact that this 'pragmatic potentiality' is codetermined by various pragmatic and conceptual factors.2
Strictly speaking, the approaches mentioned so far do not provide probability measures but only quantifications. Let us turn to probabilistic models proper. The crucial problem with probabilistic notions of any kind is to determine an adequate sample on which the computation of probability can be based. Harris rephrases Bolinger's definition by making reference to this notion:
A question of some interest is that of productivity of some elements: i.e. given an extremely large sample, with elements of classes A, B, C, etc., occurring with various members X1, X2, etc. of class X, which elements out of A, B, C have a high probability of occurring with any new member Xn, of X, and which elements out of A, B, C, etc. do not?
Those elements which have a high probability of occurring with any new Xn are called productive in respect to X.
(Harris 1960:374f, emphasis added)
The largest sample one can possibly imagine is the entirety of utterances (oral and written) in a language in a given period of time. On the basis of this sample, one could define productivity as the number of new formations in the given period, as done, for example, by Neuhaus (1973:308), who proposes the use of diachronic dictionaries such as the SOED or the OED for quantification and data collection.3 Neuhaus does not hesitate to point out that this kind of quantification presupposes the reliability of the dictionaries used, a problematic assumption to begin with. In Neuhaus (1971:140ff) some of the problems in the use of dictionary data are dis cussed, but the most outspoken criticism of this methodology can be found in Baayen and Renouf (1996), who take objection to dictionary-based approaches to productivity and make a case for the versatility of large text corpora instead. In the following, I will outline this corpus-based approach to productivity in considerable detail and return to the problem of dictionary data in Rival morphological processes 1: The productivity of verb-deriving processes, where both dictionary-based and corpus-based approaches will be used and tested in quantifying the productivity of verb deriving processes in English.
Baayen and some of his co-workers (Baayen 1989, Baayen 1992, Baayen 1993, Chitashvili and Baayen 1993, Baayen and Lieber 1991, Baayen and Renouf 1996) have developed text-corpus-based statistical measures of productivity, which has the advantage that the researcher need not depend on the perhaps insufficient recording of words by dictionary makers. Instead, such measures rely on the existence of more or less representative and sufficiently large samples of computerized texts. What counts as sufficiently large cannot be determined exactly, but it seems that even relatively small corpora like the Dutch Eindhoven Corpus (600,000 words of written text) can yield interesting results (Baayen 1992, 1993). For English, available computerized corpora such as Cobuild (originally c. 18 million words, now having been turned into the ever-increasing so-called Bank of English), or the British National Corpus (c. 100 million words), can certainly be considered large enough.
Apart from the notion of 'pragmatic potentiality/degree of exhaustion' already discussed above, two central productivity measures are proposed in the said studies, namely 'productivity in the narrow sense (P) and 'global productivity (P*)
Given a suitable text corpus, the productivity in the narrow sense Ρ of a morphological process is defined by Baayen and his co-workers as the quotient of the number of hapax legomena n1 with a given affix and the total number of tokens Ν of all words with that affix.
(1) P = n1/N
Baayen and Lieber (1991:809-810) explain the idea behind Ρ as follows. "Broadly speaking, Ρ expresses the rate at which new types are to be expected to appear when Ν tokens have been sampled. In other words, Ρ estimates the probability of coming across new, unobserved types, given that the size of the sample of relevant observed types equals N."
Ρ makes crucial reference to the notion of 'hapax legomena' (or 'hapaxes' for short), which are words that occur only once in the corpus. But why should hapaxes, i.e. the new, unobserved types, tell us anything about productivity? After all, the new, unobserved types could only be rare words, and not neologisms.
In a sufficiently large corpus, the number of hapaxes in general approximates half the observed vocabulary size (e.g. Zipf 1935). Chitashvili and Baayen (1993:57) call this kind of distribution 'Large Number of Rare Events' distribution. They show that the frequency spectrum of whole texts closely resembles the frequency spectrum of productive morphological categories, and that productive morphological categories play a crucial role in anchoring a text in the Large Number of Rare Events zone (Chitashvili and Baayen 1993:126-132). Unproductive morphological categories show a completely different frequency distribution (cf. Chitashvili and Baayen 1993: 80-86,125-126 for the difference between productive nominal -ness and unproductive verbal en-). The crucial assumption now is that the number of hapaxes of a given morphological category correlates with the number of neologisms of that category, so that hapaxes can be seen as some kind of indicator of productivity. Let us look at this assumption in more detail.
Baayen and Renouf (1996) try to illustrate the correlation between the number of neologisms and the number of hapaxes by checking whether the hapaxes are listed in a reasonably large dictionary, choosing Webster's Third as a frame of reference. Given the size of their text corpus (c. 80,000,000 words), they expect a large number of words in the corpus not to be listed in this dictionary. Furthermore, they expect that the proportion of non-listed words is highest among the hapaxes, which would substantiate the assumption that the number of hapaxes in a corpus reflects the number of neologisms. These expectations are born out by the facts. With -ness and -ity, for example, about half of the hapax legomena are not listed in Webster's Third, a proportion that significantly decreases with words occurring 2, 3, 4, and 5 times in the corpus (Baayen and Renouf 1996:76). In other words, the fewer tokens of a given type are attested, the more likely it is that the type is a neologism.
The validity of this comparison of hapaxes with Webster's Third might, however, be called into question. First of all, it is unclear whether one can rely on a dictionary like Webster's Third as a frame of reference for the novelty of a given word. Webster's Third does not aim at complete coverage (unlike the OED), nor is it clear on which basis items are selected for inclusion into the dictionary. To the contrary, the inclusion of an item into any dictionary must necessarily be arbitrary to a greater or lesser extent, so that the entries in a desk dictionary like Webster's Third can hardly be regarded as a representative sample. Combining both dictionary and corpus data in a statistical study is therefore "somewhat unfortunate", as Baayen and Renouf admit themselves (1996:77), especially since there is no common sampling scheme for the dictionary-based and corpus-based counts. Hence, Baayen and Renouf focus on lexical innovation with reference to hapax legomena.
But even if one does not believe in the reliability of these comparisons of hapaxes with dictionary entries, there are strong psycholinguistic arguments for the assumption that the proportion of neologisms among attested types increases with decreasing type frequency. As already mentioned above, high-frequency words are more likely to be stored in the mental lexicon than are low-frequency words (Rubenstein and Pollack 1963, Scarborough et al. 1977, Whaley 1978). Baayen and Renouf write that…
If a word-formation pattern is unproductive, no rule is available for the perception and production of novel forms. All existing forms will depend on storage in the mental lexicon. Thus, unproductive morphological categories will be characterized by a preponderance of high frequency types, by low numbers of low-frequency types, and by very few, if any, hapax legomena, especially as the size of the corpus increases. Conversely the availability of a productive word-formation rule for a given affix in the mental lexicon guarantees that even the lowest frequency complex words with that affix can be produced and understood. Thus large numbers of hapax legomena are a sure sign that an affix is productive.
(Baayen and Renouf 1996:74)
Having established the versatility of the use of hapaxes for productivity studies, let us turn to another problem of P, which lies in the determination of the condition "with a given affix".
For the calculation of Ρ (and the other measures) it is necessary to count all words with a given affix in the corpus. This looks like a rather straightforward task but in practice this may involve complex decisions, pivoting around two problems. The first is to determine which words can be considered to bear the affix in question, the second is to control for cohort effects in multiple affixation.
Derivatives featuring -ness, for example, are relatively easy to sort out because of the low degree of lexicalization. Other affixes, however, have adopted all kinds of idiosyncracies which opacify the relationship between the potential elements. Consider the suffix -ity in contrast, which occurs in transparent forms like opacity but also in words like entity, quantity, celebrity. It is doubtful whether the latter forms should be considered morpho logically complex at all (after all, they were most probably borrowed un analyzed). If not, one should not count them as "words with that affix". However, if one excludes them from the count, one blurs the effect that less transparent processes have more high-frequency types and fewer hapaxes. Thus the exclusion of opaque forms leads to a higher productivity value Ρ than one would probably want to have.
Alternatively, in a very generous count one could define the affix etymologically, so that even the above-mentioned derivatives must be included. In this case it is equally unclear whether this yields a desired effect, since the existence of a potentially large number of old, lexicalized, non-transparent words may blur the productivity of a potential modern process. Of course, it remains to be empirically tested whether the described sampling methods really yield statistically significant differences in their results.
The second problem concerns the sampling of multiply affixed words. Take, for example, the suffix -ize in combination with -able in a word like conventionalizable. Let us suppose this is a hapax legomenon, and let us further suppose that the base verb conventionalize is not attested elsewhere in the corpus. Should one count conventionalizable also as a hapax belonging to the category of -ize derivatives? I am inclined not to do so, since it seems reasonable to partition the lexicon into disjunct classes in order to be able to compare measures across affixes. According to this rationale one should only count the affix that has been attached last, i.e. in the case of our example conventionalizable we would assign the word to the class of -able only. A minor problem might lurk even here because sometimes it is not clear which affix was 'last' in the case of prefixes and suffixes in one derivative. Leaving this problem aside, a more serious one emerges, that of category-changing inflectional suffixes like -ing or -ed which can be used to derive adjectives from verbs. It is not clear to me whether these affixes should be ignored, just like other inflectional affixes. Thus a token like 3rd person singular conventionalizes certainly counts as a member of the category of -ize words. But what about a possible adjective conventionalized. Is this a case of a derivational suffix -ed or a case of an inflectional (participial) suffix -ed? In the first case the token would not be counted under -ize but under -ed, in the second case the token would be counted under -ize, and not under -ed.
Unfortunately, these serious methodological problems are nowhere discussed by the above-mentioned authors, so that one does not even get to know on which basis the words were counted and the measures calculated. The reason for this neglect may be partly explained by the authors' potential belief that the affixes dealt with are unproblematic with respect to the questions just raised.4 Be that as it may, as we will see in more detail in Rival morphological processes 1: The productivity of verb-deriving processes, the English verbal suffixes are a case where these methodological problems cannot be neglected.
What this discussion shows is that even 'purely' quantitative approaches cannot do without qualitative decisions. Needless to say, these decisions rest on certain theoretical assumptions that, in turn, presuppose certain concepts of productivity. In particular the decision to exclude opaque forms like entity crucially rests on the assumption that it is not a productive formation, but a lexicalized form. Hence by excluding non-productive formations we - to some extent - pre-judge the issue whether -ity is productive. The significance of such a pre-judgment may however be reduced through the use of complementary measures of productivity. In particular, the exclusion of opaque forms may lead to an increase of productivity in the narrow sense P, but to a decrease of global productivity (see below). In summary, we can say that although the rationale behind Ρ is quite convincing, one has to put up with some methodological problems.
Assuming the versatility of hapaxes for research on productivity, and further assuming that the difficulties of determining relevant tokens and types can be overcome, the productivity of an affix can now be easily calculated and interpreted. A large number of hapaxes leads to a high value of P, thus indicating a productive morphological process. On the other hand, large numbers of high frequency items lead to a high value of N, hence to a decrease of P, indicating low productivity. These results seem to be exactly in accordance with our intuitive notion of productivity, since high frequencies are indicative of the less-productive word-formation processes (Anshen and Aronoff 1988, Baayen and Lieber 1997).
However, van Marie (1992) correctly remarks that sometimes the formula leads counterintuitive results. For example, the productivity measure Ρ for the gender-neutral personal noun forming Dutch suffix -er ranks 3.5 times higher than that of its marked counterpart of female personal names in -ster, a rather unexpected and undesired result.5 Similarly, the suffix erd receives the highest value of Ρ of all processes investigated (Baayen 1992:123), although its productivity is doubtful. What is most irritable is that the value of Ρ for -erd is twice as high as that of nominal compounding (Ν N), although the latter is normally considered to "exhibit a more or less 'automatic' kind of productivity" (van Marie 1992:154).
In his reaction to van Marie's critique, Baayen (1993) seeks to counter balance such undesired results by elaborating the second measure of productivity, 'global productivity', which he had originally (Baayen and Lieber 1991, Baayen 1992) introduced as a bi-dimensional measure with the degree of productivity Ρ on the horizontal axis and the extent of use V, i.e. the number of different types with a given affix in the corpus, on the vertical axis. In the case of -erd and N-N-compounds, V is extremely low for -erd and extremely high for compounds (6 vs. 4277 types in the Dutch Eindhoven Corpus of 600,000 words of written text), which shows that the extent of use is much higher for compounding, which correctly reflects our intuition. For a better illustration of global productivity consider the following graph for a number of English word-formation processes (see Baayen 1992:124, see also Baayen and Lieber 1991:819). The global productivity is calculated on the basis of the CELEX database.6 The degree of productivity Ρ is plotted on the abscissa, the extent of use V on the ordinate.
Figure (1) 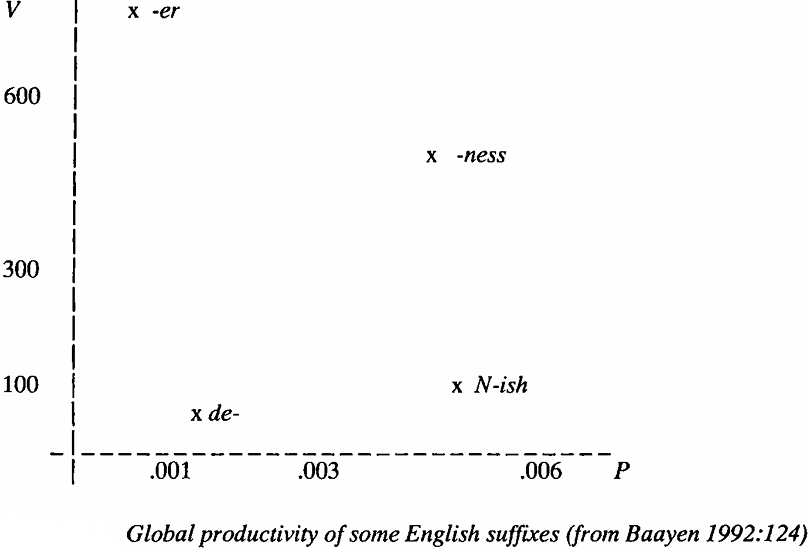
Figure (1). can be interpreted as follows. The suffix -ness has a high global productivity whereas de- or -ment have a rather low global productivity, i.e. -ness is both often used and there is a high probability to encounter new formations, whereas -ment and de- formations are rarely used and less likely to be used to coin a new word. The affix -er is often used, but is only rarely employed in new formations, and a suffix like denominal -ish is versatile in the creation of new forms but occurs only very rarely in the corpus. But what does this tell us? How can we assess the global productivity of processes when differences between them occur along both dimensions?
Baayen himself points out that global productivity as a bi-dimensional measure has the serious disadvantage that "in general it is unclear how to evaluate the different contributions of Ρ and V to the global productivity when arbitrary affixes are compared" (1992:123). This has the negative consequence that affixes cannot be ranked on a (mono-dimensional) scale according to their global productivity. In mathematical terms, this deficiency is due to the fact that the function g(V Ρ) is left unspecified, so that P* cannot be calculated, which makes comparison impossible.
Baayen (1993:192-193) therefore proposes a mathematical function for P* on the basis of seemingly complicated mathematical operations. The outcome of these operations is, however, not complicated at all. Baayen suggests that the global productivity P* should be calculated as the quotient of the number of hapaxes with a given affix and the total number of hapaxes of arbitrary constituency in the corpus. Since the latter number is constant for all categorially-determined hapaxes of any kind, the global productivity measure boils down the number of hapaxes with a given affix, already familiar to the reader as an ingredient of our productivity in the narrow sense. Baayen himself seems to be somewhat ashamed of the simplicity of this measure of global productivity, because in his comparative table of P* for a number of Dutch and English affixes he does not speak of the number of hapaxes with a given affix, although this is what the table shows, but labels the pertinent columns "Ρ* · hE" (Baayen 1993:193), i.e. the product of P* and the number of all hapaxes in the English corpus. According to his own definition, P* · hE equals the number of hapaxes with a given affix.
For an evaluation of Ρ* let us consider some of the figures in more detail. For the English person noun forming suffix -ee, for example, the number of hapaxes, and therefore its global productivity P*, is lowest of all affixes dealt with in Baayen (1993).7 However, the suffix's productivity in the narrow sense Ρ is rather high, in fact highest of all deverbal noun-forming suffixes in figure one above, since the proportion of hapaxes among all tokens with this suffix is high. How can these contradictory findings be reconciled? Is -ee a productive or an unproductive process? Baayen suggests that the two measures should be seen as "complementary measures, the primary use of Ρ being to distinguish between unproductive and productive processes as such, P* being especially suited to ranking productive processes" (1993:194).
The idea that P* should primarily be used for ranking productive suffixes is reasonable since P* can be viewed as a measure for the contribution of a particular morphological category to the expansion of the vocabulary (measured through the number of hapaxes in a corpus). Thus taking all new words, it is certainly interesting to see the extent to which certain processes contribute to the overall vocabulary growth.
The use of Ρ to distinguish between productive and unproductive processes, however, is more problematic since Ρ expresses the probability of encountering new formations of a given type, and as such only provides a continuum of more or less productive processes. Where on this continuum the productive processes end and the unproductive start, remains to be determined (if it can be determined at all).
We are now in a position to summarize and evaluate Baayen's approach to productivity. It should have become clear that, inspite of some remaining methodological problems, the different measures V, I, P, and P* have the great advantage that they make certain intuitive aspects of morphological productivity explicit and calculable. In particular, the aspects are
- the number of forms with a given affix ('extent of use' V in Baayen's terms),
- the degree of exhaustion ('pragmatic potentiality' I),
- the probability of encountering new formations ('productivity in the narrow sense' P) and
- the number of new formations in a given corpus or period ('global productivity' P*).
The separation and mathematical formalization of these aspects can be seen as a significant elaboration of Corbin's (1987:177) useful distinction between three aspects of productivity, namely what she calls profitability, regularity, and availability.8
According to Corbin's definition, a process is 'profitable' if the number of attested derivatives or potential bases is comparatively high. This is roughly equivalent to two of Baayen's measures, extent of use and pragmatic potentiality. The advantage of separating these two aspects should have become obvious during the above discussion.
A process is 'regular' if shape and meaning of the derivatives are highly predictable. Although the idea of regularity is not directly expressed in Baayen's mathematical formulae, this property is part of the rationale of the definition of productivity in the narrow sense. Thus, Ρ allows to register the effects of (semantic and phonological) transparency, because transparency is negatively correlated with frequency. As discussed in some detail above, "Categories with less transparent items will, due to this correlation, show up with more high frequency types" (Baayen 1993:194). Therefore, less regular processes in Corbin's sense will have more high frequency types, which in turn lead to a low value of productivity in the narrow sense.
Finally, a process is 'available' if it can be used to create new words. This notion is encapsulated in Baayen's global productivity and productivity in the narrow sense.
Although Corbin's trichotomy was a considerable step forward in coming to grips with the notion of productivity, Corbin did not try to arrive at a quantitative assessment of productivity in terms of this trichotomy. The importance of Baayen's work lies in the fact that with his measures the different aspects of productivity can be brought to light by explicit quantitative operations. Thus, the measures do away with notoriously ill-defined notions like semi-productivity. Given the advantages of the proposed measures, it is somewhat surprising that the work of Baayen and his collaborators has not yet lead to a proliferation of quantitative studies of productivity, inspite of the easy availability of large text corpora.
In Rival morphological processes 1: The productivity of verb-deriving processes I will implement Baayen's and Neuhaus' productivity measures for a notorious problem of English derivational morphology, viz. verb-deriving processes. Some of the merits and limitations of quantitative approaches to productivity will then become more evident than in this necessarily brief overview.
I will close this Topic with a caveat concerning quantitative approaches to productivity. Although such approaches are useful in many respects, they leave one important question open. Having quantitatively assessed that a process is more productive than another one, the obvious question is, what is the reason for this state of affairs? Which factors are responsible for the relative productivity of a process?
Kastovsky (1986) has argued that there are two aspects of productivity which should be kept apart, the 'scope' and the 'application rate' of a rule. He defines 'scope' as "the degree of semantic specificity of their output and the number and quality of the restrictions that have to be imposed on a given rule" (1986:586), while the 'application rate' is the degree to which speakers make use of a grammatical possibility. Competing terms for this latter notion are 'actuation' (van Marie), or 'probability of application' (Booij 1977:166). It is clear that quantitative measures of productivity can only aim at accurately describing the different aspects of the application rate, and not the scope of a process. Crucially, however, the scope of a rule certainly influences its application rate. The measures are therefore only a more or less accurate statement of the problem and not a solution to it. They constitute the starting point for further, much more interesting investigations into the nature of the mechanisms that restrict morphological processes.
Word formation processes are never totally unrestricted, and even the most productive affixes seem to be subject to certain structural constraints. For example, an affix may only attach to bases of a certain syntactic category or of a specific phonological or morphological make-up. Semantic factors can play a restrictive role, and the fashionableness of an affix is also dependent on extra-linguistic influences. I will provide a survey of these restrictions and their significance for English derivational morphology.
1 The relevant statistical models include Zipfs law, and the extended Yule-Simon law. An examination of the intricacies of these models is not necessary for our purposes. The interested reader is referred to Baayen (1989, 1992) for discussion.
2 That extra-linguistic factors may influence the degree of exhaustion of a rule has been frequently pointed out in the literature. Adams, for example, includes the phrase "when occasion demands" (1973:197) in her definition of productivity cited in note 13 above.
3 Neuhaus (1971:154-156, 1973:309-317) suggests yet another related measure, namely the proportion of new derivatives of a given type among all lexical innovations in the given period. Since the latter number is constant for all derivational patterns of that period this measure is only a notational variant of the number of new types in that period. In a diachronic perspective, the measure is nevertheless interesting because it shows the increase in the use of a certain process in relation to the overall growth of the vocabulary.
4 Baayen and Renouf (1996) treat in-, -ity, -ly, -ness, un-, Baayen and Lieber (1991) probably largely trusted the parsings done by the CELEX staff.
5 See van Marie (1985) for an overview over derived personal nouns in Dutch.
6 The calculations are not directly based on a text corpus, but on the CELEX lexical data base (Baayen et al. 1993), whose English part is in turn based on the Cobuild corpus. It is important to note that the figures presented in Baayen (1992), and also those in Baayen and Lieber (1991) and Baayen (1993), have turned out to be fundamentally flawed, due to a serious deficiency of the CELEX corpus: many low-frequency items of the Cobuild corpus did not make it into the CELEX data base. Unfortunately, this was un-known to these authors at the time of writing. For some discussion of this, see Baayen and Renouf (1996:92, note 13). Future users of CELEX should be aware that later versions of the CELEX corpus have the same shortcoming. Thus, in my 1994 version of CELEX (version 2.5) I find three hapaxes of -ize derivatives, while Baayen and Lieber (1991:822) have only one, I have two be- derivatives with verbal bases as against zero in Baayen and Lieber, one -ify as against zero, two de- as against three, and so forth.
For simply illustrating the concept of global productivity in figure 2.1. the incorrectness of the CELEX figures can be disregarded.
7 The affixes mentioned are -ness (77 hapaxes), -ation (47), -er (40), -ity (29), -ment (9), -ian (4), -ism (4), -al (3), -ee (2). Note again, that these figures are flawed to an unknown extent due to the use of CELEX. For the purposes of our discussion the inaccuracy of the figures is not relevant, since the parallel figures for Dutch are correct, and they raise the same questions. This also suggests that the error rate in the CELEX data base is evenly distributed across different affixes.
8 The original French terms are "rentabilité", "regularité" and "disponibilité". The English equivalent terms are taken from Carstairs-McCarthy (1992:37).
|
|
|
|
يجب مراقبتها بحذر.. علامة في القدم تشير إلى مشاكل خطيرة
|
|
|
|
|
|
|
العلماء يحلون لغز بركان أدى إلى تجمد الأرض قبل 200 عام
|
|
|
|
|
|
|
رئيس جلسة العلوم الهندسية: بحوث مؤتمر جامعة الكفيل تقدم حلولًا عملية قابلة للتطبيق
|
|
|