المعادلة (8–4) لها نتائج مهمة عند تطبيقها على مسألة القوة المركزية؛ أي الجسيم المتحرك بتأثير قوة متجهة دائمًا لنقطة ثابتة.

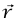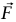إذا أخذنا نقطة الأصل O عند هذه النقطة الثابتة، فإن العزم يتلاشى؛ لأن  و  متوازيان في نفس الاتجاه (أو متوازيان بعكس الاتجاه)؛ وبالتالي فإن 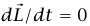، وتكون كمية التحرك الزاوية  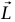ثابتة. ثبوت  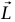يقتضي ضمنًا أنْ:

(أ) تقع حركة الجسيم في مستوى ثابت، يسمى المستوى المحتوي على مركز القوة، والموضع الابتدائي للجسيم، ومتجه السرعة الابتدائي للجسيم.

(ب) يمسح المتجه الواصل من مركز القوة إلى الجسيم مساحات بمعدل ثابت (هذا هو قانون كبلر الثاني، وهو خاصية لجميع القوى المركزية، وليس فقط لقانون التربيع العكسي)؛ وهذا مع حركة الجسيم في هذا المستوى.

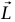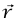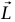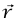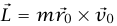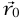لإثبات (أ)، نمرر مستوى خلال مركز القوة O عموديًّا على المتجه الثابت . تقتضي المعادلة (8–2) ضمنًا أن يكون  عموديًا على ؛ وبالتالي فإن  يقع في المستوى. لكن بما أن  (حيث  و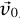 هما متجها الموضع والسرعة الابتدائيان)، فإن المستوى العمودي على  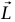يكون هو المستوى الذي يحتوي على 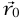و.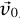

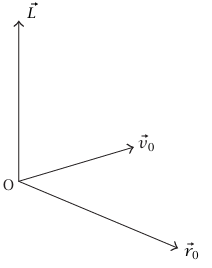
شكل 1–8: اتجاه .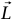

في إثبات (أ)، استخدمنا فقط حقيقة ثبوت اتجاه 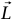. مقدار 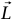ثابت أيضًا. باستخدام تعريف الضرب المتجهي، نجد أن مقدار  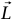هو:

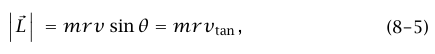
حيث الزاوية θ بين 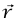 و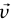، وv sin θ = v_tan السرعة المماسية (أي مركبة السرعة العمودية على 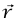). المساحة المظللة في شكل 8–2 هي المساحة التي يمسحها المتجه  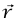في الفترة الزمنية الصغيرة Δt. تكون المساحة خلال قيم الدرجة الأولى في Δt هي ΔA = (1/2) rv_tan Δt؛ وبالتالي فإن المعدل الذي تمسح به المساحة هو
dA/dt = (1/2) rv_tan = L/2m ولأن L ،ثابتة، فإن dA/dt ثابتة.

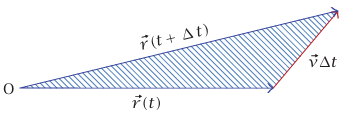
شكل 8–2: مساحة ممسوحة بواسطة المتجه النصف قطري.

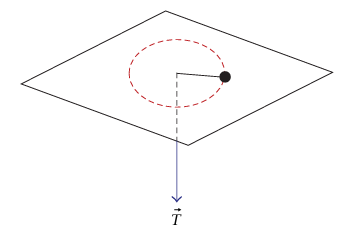
شكل 8–3: جسيم يتحرك على منضدة أفقية في مسار دائري محافظ عليه بواسطة شد في الوتر المربوط في الجسيم في مثال 8–1.

مثال 8–1 (جسيم يتحرك على مستوى أفقي في مسار دائري). جسيم كتلته m يتحرك على سطح منضدة أفقية ملساء، مقيد بوتر يمر خلال ثقب في المنضدة (شكل 8–3). في البداية يتحرك الجسيم بسرعة مقدارها v₁ في دائرة نصف قطرها r₁. يُسحب الوتر ببطء حتى يتحرك الجسيم في دائرة أصغر نصف قطرها r₂. احسب:

(أ) مقدار سرعة الجسيم الجديدة v₂.

(ب) النسبة T₂/T₁ (حيث T₁ وT₂ هما الشدان الابتدائي والنهائي في الوتر).

(جـ) الشغل المبذول على الجسيم بواسطة الوتر.

الحل. القوة التي يؤثر بها الوتر على الجسيم موجهة دائما نحو الثقب؛ وبالتالي تكون كمية التحرك الزاوية محفوظة؛ أي إن v₁r₁ = v₂r₂؛ وبالتالي فإن v₂ = v₁ (r₁/r₂). وبما أن T = mv²/r فيكون لدينا:

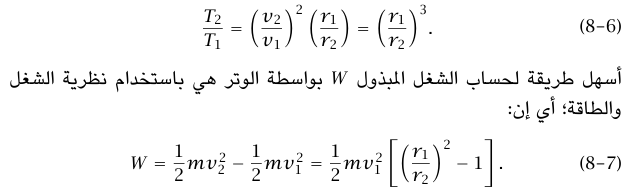
من المفيد أيضًا تعليميا حساب الشغل مباشرة من تعريف 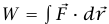 (لاحظ أن الشد في الوتر يتغير مع سحب الوتر لذلك لا نستطيع التعامل مع القوة على أنها ثابت). في اللحظة التي يكون عندها طول الوتر (من الثقب إلى الجسيم) r، يكون الشد (من المعادلة (6–8)) ³(T = (mv₁²/r₁) (r₁/r، والقوة المؤثرة على الجسيم 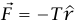؛ حيث 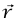 متجه وحدة يشير في الاتجاه الخارج من نقطة المركز عند تغيير طول الوتر من r إلى r + dr (لاحظ أن dr سالبة عند تقصير الوتر)، تكون إزاحة الجسم هي  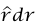مجموع عليها مركبة مماسية لا تساهم في الشغل؛ وبذلك يكون:

وذلك بالاتفاق مع المعادلة (7–8).

بالإضافة إلى ذلك، إذا طبقنا نظرية الشغل والطاقة على العملية المتناهية الصغر التي يتغير فيها طول الوتر من r إلى r + dr ويتغير مقدار سرعة الجسيم من v إلى v + dv، نجد أن (mv²/r)dr = (1/2)m(v + dv)² – (1/2)mv²– مما يؤدي إلى dr/r = – dv/v؛ وبذلك يكون 0 = (d(lnv + lnr مما يقتضي ضمنًا أن يكون
lnv + lnr = const؛ أي إن vr = ثابت، وهو نص حفظ كمية التحرك الزاوية. الميكانيكا بنية منطقية أنيقة ومتناسقة.