


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-02-29
التاريخ: 15-9-2020
التاريخ: 15-9-2020
التاريخ: 3-12-2020
|
إذا كانت القوة على جسيم هي  فإن الشغل المبذول على الجسيم عندما يتحرك من x0 إلى xf هو اعتبر المسار متتالية من خطوات صغيرة
فإن الشغل المبذول على الجسيم عندما يتحرك من x0 إلى xf هو اعتبر المسار متتالية من خطوات صغيرة  )
)
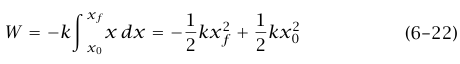
(لاحظ أن القوة محافظة؛ لأن الشغل يعتمد فقط على نقطتي البداية والنهاية ولا يعتمد على ما إذا كان الجسيم تحرك مباشرة من x0 إلى xf أو تراجع في مساره.) تنص نظرية الشغل والطاقة على:
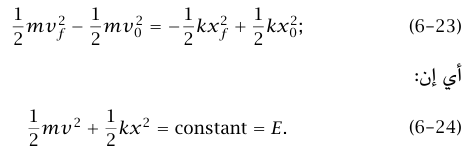
المعادلة (24–6) متضَمَّنة بالفعل في حلنا السابق. تذكر أن (δ –x = xmax cos (ωt و(δ – v = – ωxmax sin (ωt. باستخدام ω2 = k/m وmو1 = δsin2 δ + cos2، نحصل على:

ولأن vmax = ωxmax، يمكننا كتابة الطاقة على الصورة (1/2)mvmax2 أو (1/2)kxmax2. ندرك أن (1/2)kx2max هي طاقة الجهد عندما تكون نقطة المرجع هي موضع الاتزان (0 = x). التعبيران السابقان للطاقة يناظران حالتي وجود الجسيم عند 0 = x، عندما تكون طاقة حركته قيمة عظمى ولا يكون له طاقة جهد، أو عند x = ± xmax عندما تكون طاقة جهده قيمة عظمى ولا يكون له طاقة حركة.

أي شخص لم يسمع قط عن الطاقة ولديه رؤية رياضياتية قد يدرك أنك إذا قمت بضرب طرفي المعادلة (2–6) في dx/dt تحصل على
d/dt ((1/2)mvmax2 + (1/2)kxmax2) = 0، وهي مماثلة للمعادلة (24–6) الأكثر من ذلك، إذا كان x0 وv0 معينين فإن المعادلة (24–6) تعطي v كدالة في x. وبما أن (dt = dx/v(x، فيمكنك إجراء التكامل للطرفين للحصول على t(x) وبالتالي x(t).



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|