المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | ترتيب تصاعدي Ascending Order |
 1650
 10:29 صباحاً
التاريخ: 3-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 74|
أقرأ أيضاً
التاريخ: 22-11-2015
1123
التاريخ: 13-12-2015
1439
التاريخ: 11-1-2016
2020
التاريخ: 29-12-2015
1222
|
يرتبط هذا الترتيب بالمشاهدات كمفردات عند إيجاد الوسيط Median فلإيجاد الوسيط للمشاهدات 15 , 22 , 27 , 25 , 21 , 24 , 20 يتطلب أولاً ترتيباً تصاعدياً إذ نبدأ بالمشاهدة الأصغر بالقيمة ثم تتدرج إلى الأكبر هكذا 15 , 20 , 21 , 22 , 24 , 25 , 27 .
كما ويرتبط هذا الترتيب بدرجات (أسس) الحدود الجبرية في الاقتران كثير الحدود كما يلي .
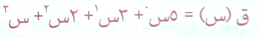
حسب قوة س الصاعدة Ascending Powers
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
