


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء| الطرق المباشرة لتعيين أطوار الانعكاسات (طرق الاحتمالات Probability methods) |
|
|
|
أقرأ أيضاً
التاريخ: 2023-10-12
التاريخ: 2023-10-07
التاريخ: 2023-09-27
التاريخ: 2023-10-12
|
الأساس الذي بنيت عليه الطرق التي سيتم شرحها فيما يلي هو البحث الذي نشر سنة 1952 بواسطة ساير Sayre على الرغم من أن نتائج رياضية مماثلة له قد نشرت فيما قبل ذلك التاريخ بحيث يمكن إثبات المعادلة التالية في حالة وجود بعض القيود.
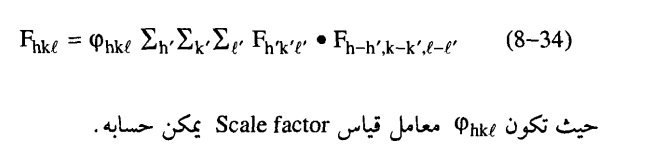
وتطبيق هذه المعادلة يعني أن أي معامل تركيبي يمكن تعيينه من حاصل ضرب معاملات التركيب لكل زوج من الانعكاسات يكون مجموع إحداثيات ميلر لها يعطي إحداثيات ميلر للانعكاس المطلوب تعيين معامله التركيبي.
أي أن المعامل التركيبي للانعكاس (213) يعتمد على حاصل ضرب F (322)، (1 1̅ 1̅) F، وكذلك (604) F، (1̅ 1 4̅) F وهكذا.
وللوهلة الأولى يعتقد أن المعادلة (34-8) غير ذات فائدة حيث يبدو أنه لتعيين قيمة F لأحد الانعكاسات لابد من معرفة القيمة العددية وكذلك زاوية الطور لكل الانعكاسات الأخرى ولكن في حالة إذا كانت قيمة Fhkl كبيرة يمكن تطبيق المعادلة الاتية:
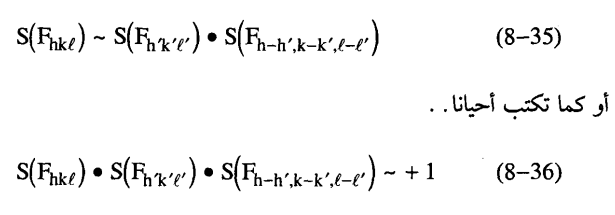
معناها إشارة «Sign» والعلامة ~ معناها احتمال أن تكون مساوية وقيم Sربما تأخذ القيمة 1+ أو 1-.
نجد أن المعادلة (35-8) هي معادلة احتمالية اشتقت من المعادلة (34-8) وهي أساس معظم عمليات تعيين أطوار الانعكاسات بالطرق المباشرة، والمعادلة (35-8) تسرى أيضا على الحالات التي يمكن أن تستخدم فيها المتباينات أي أن المتباينات تمثل الحالات التي تصبح فيها الاحتمالات مؤكدة.
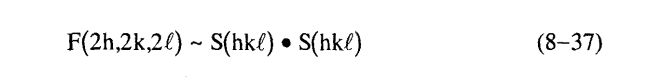
أي أنه بصرف النظر عن إشارة Fhkl فإن (2h,2k.2l)F ستكون موجبة {2(1-) أو 2(1+)ٍ} إذا كانت الانعكاسات قوية بدرجة كافية، وهذه هي نفس النتيجة التي نتوصل إليها بتطبيق المتباينات في المعادلة (20-8) ولهذا السبب فإن المتباينات لا تستخدم عمليا لأن نفس النتائج نحصل عليها بدرجة عالية من الاحتمال من المعادلة (35-8).
والسؤال ما هي قيمة الاحتمالات بدقة للمعادلة (35-8)، (37-8) يعتبر سؤالا مهما وقد درست هذه المشكلة ووضعت لها إجابات عدة.
والمعادلة التي تعطي الاحتمال والتي تستخدم غالبا هي التي استنبطها کوکران وولفسون Cochran and woolfson.
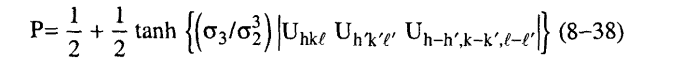
حيث p هي احتمال أن المعادلة (35-8) يمكن تطبيقها.

حيث قيم n هي المعرفة في المعادلة (25-8) وإذا كانت كل الذرات للوحدة البنائية متساوية نحصل على:

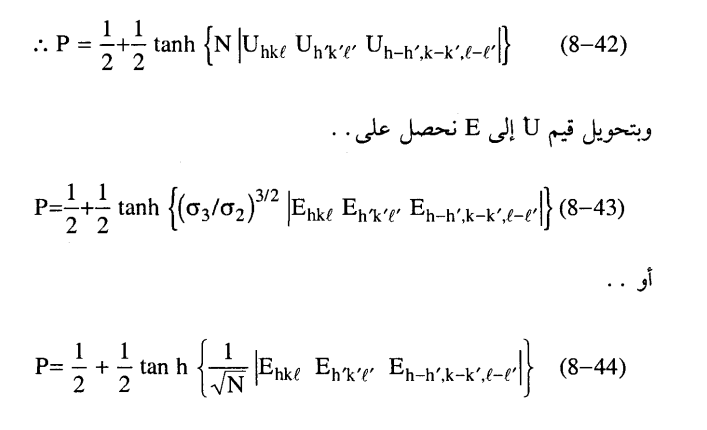



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|