
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الطيوف الاهتزازية لجزيئات ثنائية الذرة
المؤلف:
الدكتور محمد انور بطل
المصدر:
الفيزياء الذرية والجزيئية
الجزء والصفحة:
ص 374
16-2-2022
1859
الطيوف الاهتزازية لجزيئات ثنائية الذرة
إن المحاور xyz المرتبطة بتشكيلة التوازن هي نفسها المحاور المثبتة في الفضاء (z يرمز للمحور ما بين إلأنوية) ولنفرض أيضاً بأن الجزيء عبارة عن هزاز توافقي . ثم بهزاز لاتوافقي .
1 - الهزاز التوافقي:
إن سويات الطاقة محسوبة بإستخدام كمون الهزاز التوافقي وكذلك التوابع المرافقة.
قواعد الاصطفاء للإصدار وللإمتصاص:
ليكن الإنتقال بين الحالتين المميزتين ب 'v و "v وكما رأينا إن شدة هذا الإنتقال متناسبة مع مربع طويلة 2|"mv'v| وحتى يكون الإنتقال مسموحاً يجب أن يكون واحد على الأقل من مركبات m غير معدوم. وبما أنه لايوجد دوران فيعتبر محور الجزيء هو اتجاه oz الثابت في الفضاء بما أن :
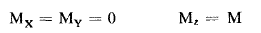
إذاً يمكن أن نكتب قاعدة الاصطفاء التي نجعل العلاقة التالية غير معدومة :
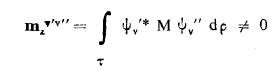 ........(1)
........(1)
a) - حالة جزيئات ثنائية الذرة heteromacleaire :
لننشر M بسلسلة بالنسبة لp :
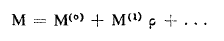 ........(2)
........(2)
حيث نرمز Mo للعزم المستمر ( الدائم ) و:
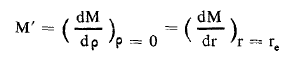 ........(3)
........(3)
بتعويض 3و 2 في 1 نجد:
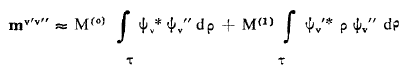
الحد الأول من الطرف الأيمن معدوم لأن 'ψv و "ψv متعامدان وبالتالي فإن قاعدة الإصطفاء تكتب:

أي سيكون الإنتقال مسموح (اصدار أو امتصاص) إذا تحقق الشرطان :
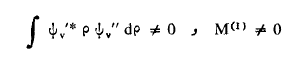
أي أن الشروط الأول هو أن يكون هناك تغير في عزم ثنائي القطب أثناء الإهتزاز وهذا محقق في حالة هذا النوع من الجزيئات وبالتالي محقق إذا كان 1 + ''v' =v أو 1 + ''v' =v أي 1 ± = v أي أن :
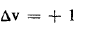
b) — حالة جزيئات ثنائية الذرة:
إن وجود مركز انعكاس لمجموعة النواتان المتطابقتان يؤدي إلى أن :
M = 0
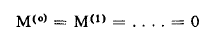
ينتج عن ذلك بأن كل الإنتقالات ممنوعة ( إصدار أو امتصاص ) في هذا النوع من الجزيئات .
طيوف الإصدار والامتصاص شكل (1) :
a) - حالة -جزيئات ثنائية الذرة hatemonuleaire :
علاقة الإصطفاء 1+ = Δv تعطي العدد الموجي
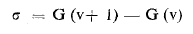
حيث يعبر عن σ ب cm-1 والشكل التالي تعطي الإنتقالات الاهتزازية نلاحظ أن كل انتقال بعد σ = ω.

الشكل (1)
b) - حالة جزيئات ثنائية الذرة homonuckleair :
لايوجد طيف اهتزازي ( امتصاص — اصدار ) .
قواعد الإصطفاء من أجل تشتت رامان:
حتى يكون هناك انتقال مسموح بين سويتين ٧ و "v فمن الضروري أن يكون واحد على الأقل من مركبات التنسور التالي غير معدومة:
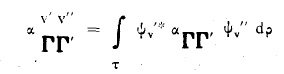 ..............(4)
..............(4)
إذا نشرنا 'αΓΓ بسلسلة :
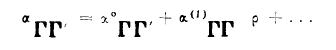 ..............(5)
..............(5)
حيث'α(o)ΓΓ مركبة الإستقطابية الدائمة بتعويض(4) في(5) نجد أن قاعدة الإصطفاء كما في حالة الإمتصاص والإصدار
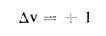
والشرط 0 ≠ 'α(o)ΓΓ محقق في الجزيئات ثنائية الذرة بنوعيها .
طيف رامان:
إن الإنزياح بالعدد الموجي لخط رامان بالنسبة للاشعاع المحرض (المحث) يعطي بالعلاقة:
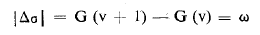
أي هناك خط مركزي وخط بعدد موجي σo - ω يدعى Stokes وخط آخر σo + ω يدعى anti - Stokes والآخر أضعف بكثير من الأول .
ملاحظة:
حسب التقريب المستخدم نلاحظ في حالة الإمتصاص فقط الإنتقال 0 ←1 وفي حالة تشتت رامان نلاحظ 0 → 1 وكذلك 1→ 0 حيث في هذه الحالات تكون اسكان سوية الطاقة معهم لأن
الشدة متناسبة مع الإسكان والأخيرة متناسبة و e-ω(1/2/+v)kT او مع e-ωv/hT .
2- الهزاز اللاتوافقي:
تكتب قواعد الاصطفاء في هذه الحالة ب :
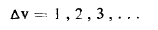
للإصدار والامتصاص وتشتت رامان وهذا يعني أن كل الانتقالات مسموحة (ماعدا الجزيئات homonule). فمثلا في حالة الإمتصاص (لجزيئات hetere ) يمكن أن نضع الإنتقال :
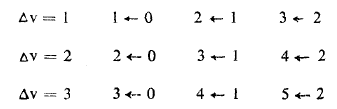
 الاكثر قراءة في الفيزياء الجزيئية
الاكثر قراءة في الفيزياء الجزيئية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















