المتذبذب التوافقي The Harnonic Oscillator

يمكن وصف الجهد V(r) بجهد قطع مكافئ لسعة الاهتزاز الصغيرة، اي للإزاحة القليلة عن مسافة الاتزان، بتقريب جيد وكما ياتي:

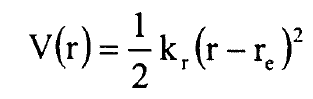..................(1)

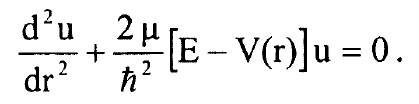........(i)

حيث الثابت Kr يساوي k_r = μω²₀ للمتذبذب التوافقي الذي تردده الزاوي ω₀ وكتلته المختزلة μ ونختار اصل اطار الاسناد بحيث r_e = 0 وبعد تحويل المتغير r الى المتغير 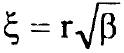نضع المعادلة (i) بالشكل:

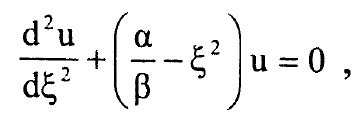...................(2)

حيث:

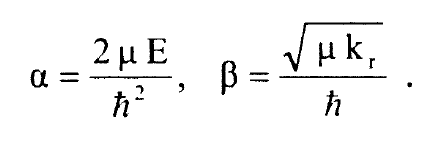
في الحالة المحددة 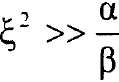، اي عندما ∞ → r ، يمكن اهمال α/β وفي هذه الحالة نستطيع كتابة الحل المقارب:

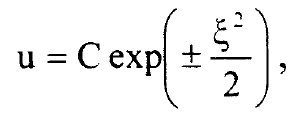...............(3)

ولان الدالة الموجية (u(ζ يجب ان تكون قيمتها محدودة عندما ∞ → ζ فان الحل بالاشارة الموجية في المعادلة 3-29 غير مقبول فيزيائيا لذلك للحل العام للمعادلة 2 (نستخدم الدالة):

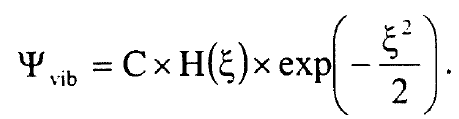.................(4)

وبعد تعويض المعادلة (4) في المعادلة (2) نصل الى المعادلة:

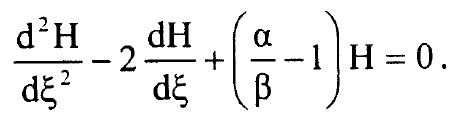....................(5)

لحل المعادلة (5) نستخدم متوالية اسية في ζ:

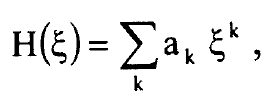............(6)

وبعد تعويض المعادلة (6) في المعادلة (5) نحصل على معادلة تكرار للمكافئات a_k:

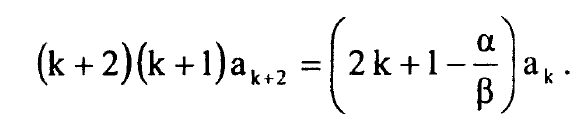.................(7)

تكون قيمة الدالة 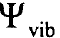محدودة اذا احتوت المتوالية (6) على عدد محدود من الحدود وهذا يعني ان المتوالية (6) يجب ان تنتهي بعد الحد 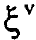وكل الحدود للقيم k> v يجب ان تساوي الصفر، لذلك فان  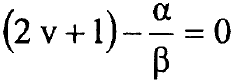في المعادلة (7) وبناء على ذلك فان طاقات المتذبذب التوافقي المسموح بها تعطى بالتعبير:

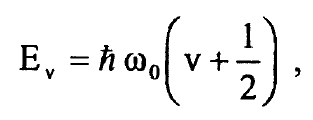.................(8)

حيث 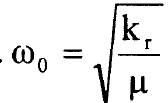ان قيم الطاقة الذاتية E_v للمتذبذب التوافقي متساوية البعد عن بعضها البعض وأوطأ قيمة للطاقة بالعدد الكمي الاهتزازي v = 0 تساوي طاقة نقطة الصفر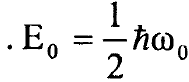

في علم الطيف تستخدم قيم الحد الطيفي 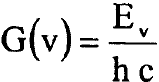بدلا من قيم الطاقة الذاتية وتكتب كما ياتي:

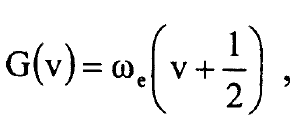....................(9)

حيث الثابت الاهتزازي 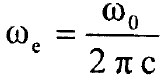يقاس بوحدات cm^-1 وc سرعة الضوء. 

من الملاحظ ان تكميم الطاقة ياتي نتيجة لان الدالة (H(ζ محدودة لكل قيم ζ يجب ان يكون ممكنا تمثيلها بعدد محدود من الحدود.

باختيار 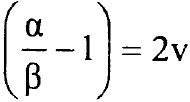 تصبح المعادلة (5) معادلة تفاضلية هيرميتية وحلها يكون بمتعددة حدود هيرمت (H(ζ. ثابت المعايرة C في المعادلة (4)  يتم اختياره بحيث 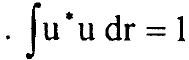في جدول 1 بعض دوال (H(ζ.

جدول 1 متعددة حدود هيرمت لأوطأ اربعة مستويات طاقة للمتذبذب التوافقي.

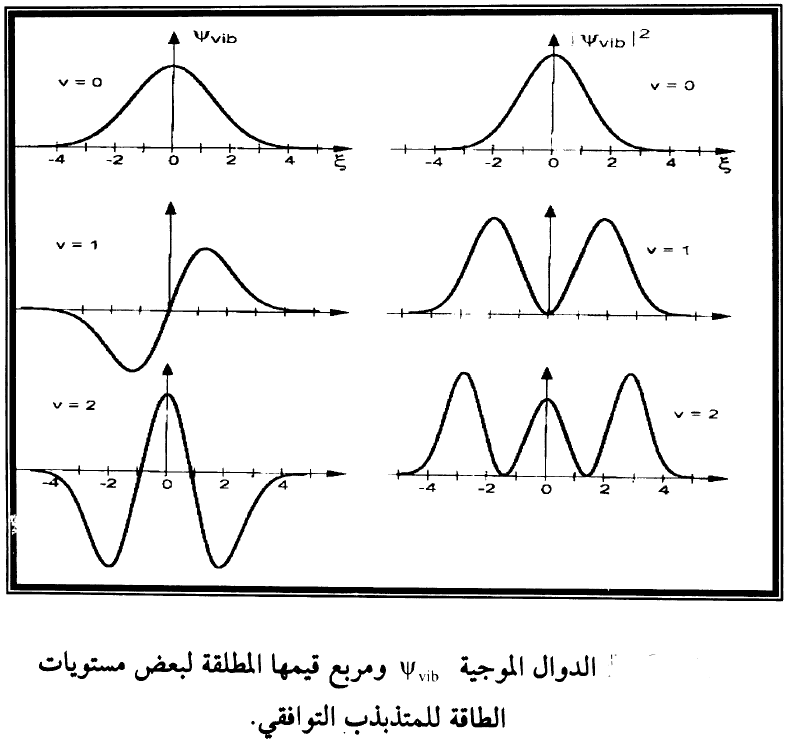
وفي شكل (1) مبين الدوال الموجية الاهتزازية:

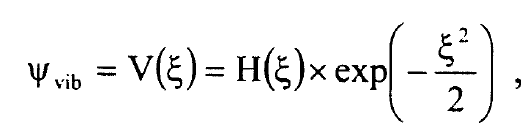
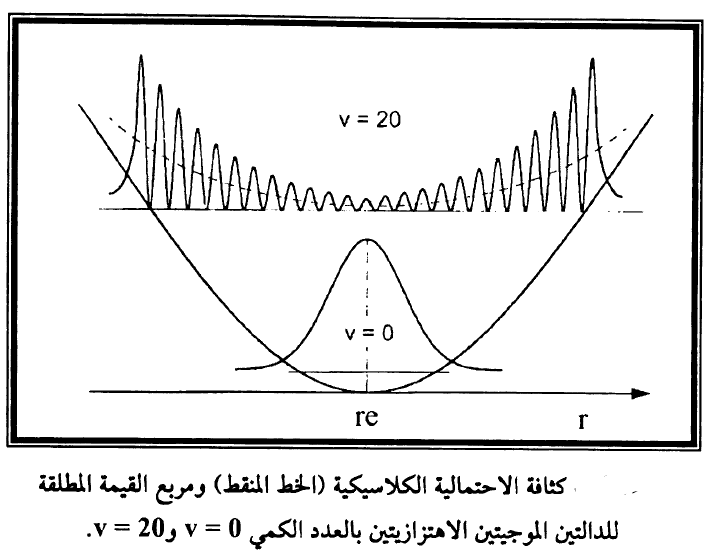
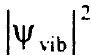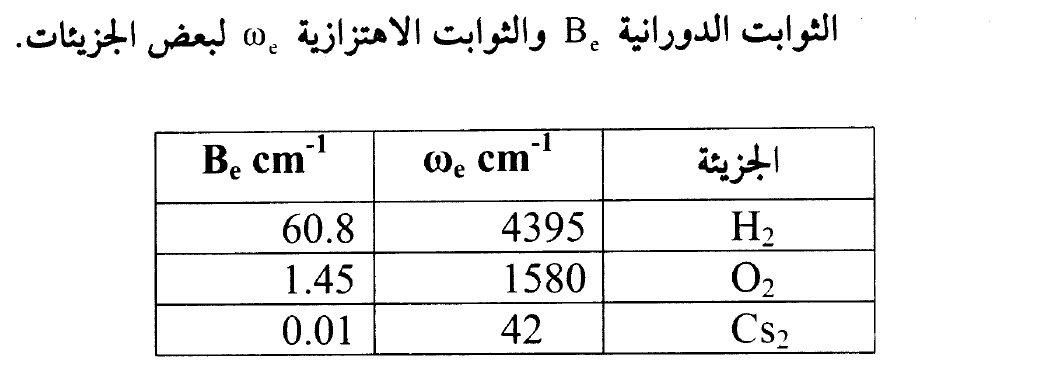
لعدد من الاعداد الكمية الاهتزازية v. لقيم v الكبيرة يصبح مقدار كبيرا بالقرب من نقاط التحول الكلاسيكي حيث يملك المتذبذب الكلاسيكي احتمالية عالية للتواجد وفقا لمبدأ التوافق correspondence principle الذي ينصل على ان وصف ميكانيكا الكم يتحول الى الوصف الكلاسيكي لقيم الاعداد الكمية الكبيرة v. وفي شكل (2) مقارنة بين احتمالية التوزيع الكمية 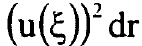والقيمة الكلاسيكية لمستويين اهتزازيين v = 0 وv = 20. لقيم v الكبيرة المنحني الكلاسيكي يشبه متوسط التوزيع الفضائي الكمي بينما يختلف الوصف الكمي كثيرا عن الوصف الكلاسيكي لقيمة v = 0. ان القيم التجريبية الاهتزازية ω_e والثوابت الدورانية B_e لبعض الجزيئات ومنه يتضح ان زمن ذبذبة واحدة ^1-(T = (ω_oc لجزيئة H₂ الخفيفة

يساوي T = 8 ×10^-15s ولجزيئة Cs₂ الثقيلة T = 8 ×10^-13s اي ان زمن ذبذبة واحدة يقع في المدى^{14 -}10-^12-10 ثانية وعلى التباين من ذلك فان زمن دورة واحدة 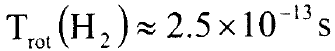 لأوطأ مستوى لجزيئة الهيدروجين H₂ يساوي 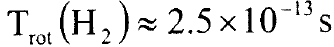ويساوي 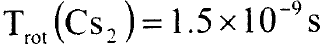لأوطأ مستوى دوران لجزيئة Cs₂،  اي أنها اكبر بمقدار مرتبتين او ثلاثة مراتب.

الجدول (1)

الشكل (1)

الشكل (2)

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

الكشف عن الألغام والمتفجرات

الكربون .. أمير المواد وعميدها

خواص المواد النانوية

تاريخ أنابيب الكربون النانوية (History of carbon nanotubes)

الاتصال والحوار العام في تطوير تقنية النانو

نشاطات المنظمات الدولية في مجال التقنية النانوية

حالة المعارف المتصلة بمخاطر المواد النانوية

الاعتبارات الأخلاقية في التقنية النانويه

المنفعة الاجتماعية للتقنية النانوية

ما المقصود بالنانو؟

النانو تكنولوجيا.. علم وصناعة القرن الجديد

أنابيب الكربون النانوية Nanotubes Carbon