
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
تقريب بورن – اوبنهايمر Born-Oppenheimer Approximation
المؤلف:
الدكتور صلاح الدين محمود يونس
المصدر:
الفيزياء الجزيئية
الجزء والصفحة:
p 36
29-9-2020
6023
تقريب بورن – اوبنهايمر Born-Oppenheimer Approximation
اقترح هذا التقريب من قبل بورن واوبنهايمر عام 1927 في الايام الاولى لميكانيكا الكم ولا يزال الى يومنا هذا من غير الممكن الاستغناء عنه في حسابات الدول الموجية الجزيئية ويضم تقريب بورن – اوبنهايمر خطوتين وفي الخطوة الاولى تهمل طاقة النواة الحركية وتدخل المواقع النووية في هاملتون الالكترونات كاعلومات فقط ولا تزال الالكترونات تحت تاثير جهد كولوم للنوى المعلقة في الفضاء ثم يجري حل معادلة شرودنجر لايجاد الدول الموجية الالكترونية مع ثبات مواقع النوى وفي الخطوة الثانية يعاد ادخال الطاقة الحركية النووية وتحمل معادلة شرودنجر للحركة النووية، ففي الخطوة الاولى نحصل على حل معادلة شرودنجر للمسالة الالكترونية لترتيب نووي ثابت وعشوائي وفي الخطوة الثانية يمكن ايجاد حل للمسالة النووية باختزال تاثير الالكتورنات الى جهد مؤثر. في تقريب بورن – اوبنهايمر كل المكافئات Cmm تؤخذ مساوية للصفر، ويهمل الترابط بين الحركة الالكترونية والحركة النووية وتصبح المعادلة بالشكل:
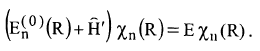 ..................(1)
..................(1)
في تقريب بورن – اوبنهايمر معادلة شرودنجر للدوال النووية (χn (R في الحالة الالكترونية n، والتي تعين سعة الاحتمالية لتواجد النواة عند الاحداثي R، تكون بالشكل:
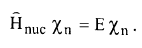 .....................(2)
.....................(2)
هذا المؤثر الهاملتوني 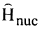 يعطى بالمعادلة:
يعطى بالمعادلة:
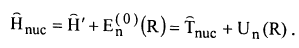 ...................(3)
...................(3)
المؤثر الهاملتوني 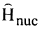 يساوي مجموع طاقة النواة الحركية والطاقة الكامنة (Un(R والتي تساوي الطاقة الكلية للجزيئة الجاسئة En(0)(R) تبين المعادلة 3 انEn(0)(R) يمكن اعتبارها كجهد Un(R) تتحرك النواة فيه. لاي حالة الكترونية Φen بطاقة En(0)(R) توجد حلول من مجمع دوال χnv والتي يمكن النظر اليها على انها الدوال النووية في الحالة الالكترونية Φen والتي تصف الحالات الاهتزازية المختلفة كما مبين بالدليل v.
يساوي مجموع طاقة النواة الحركية والطاقة الكامنة (Un(R والتي تساوي الطاقة الكلية للجزيئة الجاسئة En(0)(R) تبين المعادلة 3 انEn(0)(R) يمكن اعتبارها كجهد Un(R) تتحرك النواة فيه. لاي حالة الكترونية Φen بطاقة En(0)(R) توجد حلول من مجمع دوال χnv والتي يمكن النظر اليها على انها الدوال النووية في الحالة الالكترونية Φen والتي تصف الحالات الاهتزازية المختلفة كما مبين بالدليل v.
يفصل تقريب بورن – اوبنهايمر معادلة شرودنجر الى معادلتين مستقلتين هما:
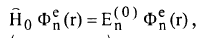 .....................(4)
.....................(4)
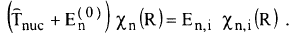 ....................(5)
....................(5)
الدالة الموجية الكلية Ψ لحالة الكترونية في تقريب بورن – اوبنهايمر يمكن كتابتها كحاصل ضرب دالة موجية الكترونية ودالة موجية نووية:
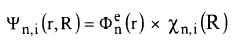
يتبين من الدالة الموجية Ψ ومن المعادلتين 4 و5 ان الطاقة الكلية En,i تتكون من جمع متوسط الطاقة الحركية النووية والالكترونية وتحتوي الطاقة الكامنة للتنافر بين النوى:
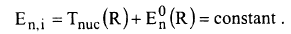
الدالة الكلية Ψ يمكن معايرتها بمعايرة المعاملات بشكل مستقل، اي ان:
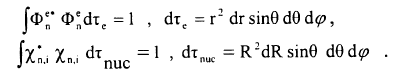
 الاكثر قراءة في الفيزياء الجزيئية
الاكثر قراءة في الفيزياء الجزيئية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















