


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-1-2022
Date: 2-1-2022
Date: 9-1-2022
|
Direct sums are defined for a number of different sorts of mathematical objects, including subspaces, matrices, modules, and groups.
The matrix direct sum is defined by
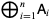 |
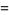 |
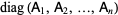 |
(1) |
 |
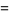 |
![[A_1 ; A_2 ; ... ; A_n]](https://mathworld.wolfram.com/images/equations/DirectSum/Inline6.gif) |
(2) |
(Ayres 1962, pp. 13-14).
The direct sum of two subspaces 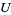 and
and 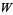 is the sum of subspaces in which
is the sum of subspaces in which 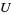 and
and 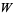 have only the zero vector in common (Rosen 2000, p. 357).
have only the zero vector in common (Rosen 2000, p. 357).
The significant property of the direct sum is that it is the coproduct in the category of modules (i.e., a module direct sum). This general definition gives as a consequence the definition of the direct sum 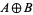 of Abelian groups
of Abelian groups 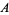 and
and 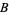 (since they are
(since they are 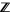 -modules, i.e., modules over the integers) and the direct sum of vector spaces (since they are modules over a field). Note that the direct sum of Abelian groups is the same as the group direct product, but that the term direct sum is not used for groups which are non-Abelian.
-modules, i.e., modules over the integers) and the direct sum of vector spaces (since they are modules over a field). Note that the direct sum of Abelian groups is the same as the group direct product, but that the term direct sum is not used for groups which are non-Abelian.
Note that direct products and direct sums differ for infinite indices. An element of the direct sum is zero for all but a finite number of entries, while an element of the direct product can have all nonzero entries.
REFERENCES:
Ayres, F. Jr. Schaum's Outline of Theory and Problems of Matrices. New York: Schaum, 1962.
Rosen, K. H. (Ed.). Handbook of Discrete and Combinatorial Mathematics. Boca Raton, FL: CRC Press, 2000.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|