


 علم الكيمياء
علم الكيمياء 
 الكيمياء التحليلية
الكيمياء التحليلية 
 الكيمياء الحياتية
الكيمياء الحياتية 
 الكيمياء العضوية
الكيمياء العضوية 
 الكيمياء الفيزيائية
الكيمياء الفيزيائية
 الكيمياء اللاعضوية
الكيمياء اللاعضوية 
 مواضيع اخرى في الكيمياء
مواضيع اخرى في الكيمياء
 الكيمياء الصناعية
الكيمياء الصناعية |
أقرأ أيضاً
التاريخ: 14-9-2020
التاريخ: 22-10-2020
التاريخ: 30-12-2021
التاريخ: 2025-01-20
|
All of the threonine stereoisomers 19-22 are chiral substances; that is, they are not identical with their mirror images. However, it is important to recognize that not all diastereomers are chiral. To illustrate this point, we return to the tartaric acids mentioned previously in connection is Pasteur's discoveries .

Proceeding as we did for threonine, we can write four projection formulas for tartaric acid, 2,3-dihydroxybutanedioic acid, as shown by 23-26:
Figure 5-13.)
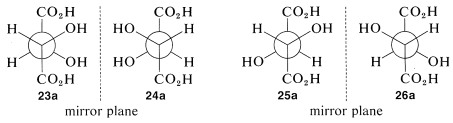
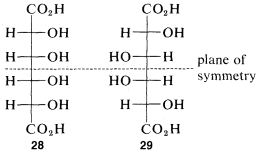
There are two pairs of mirror images 23a and 24a, as well as 25a and 26a. However, what will not be so immediately clear, but what you must verify for yourself is that 25a and 26a are, in fact, identical. This means that 25a and 26a are representations of a single achiral substance, identical with its mirror image. Substances that have chiral centers but are themselves achiral are called meso compounds.
The condition that makes possible the existence of meso compounds is an appropriate degree of molecular symmetry. There are several kinds of such molecular symmetry. In the case of projection formulas 25 (or 26) there is a plane of symmetry, which means that a plane can be placed through the molecule such that one half of the molecule is a mirror image of the other half. The mirror plane for meso-tartaric acid can be seen easily from its projection formulas 25b and 26b. These two formulas are superimposable if one is rotated 180o in the plane of the paper.
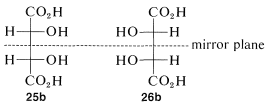
The Newman representations 25a and 26a of meso-tartaric acid does not have a mirror plane. Why is it different from the Fischer projections in this respect? The reason is that the projection formulas represent a particular eclipsed conformation 27 of meso-tartaric acid that does have a mirror plane:
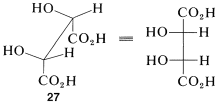
Therefore, if you are confronted with a particular sawhorse or Newman formula and you have to decide whether it represents a meso compound, the best procedure is to make a ball-and-stick model of the conformation and then rotate around the bonds to see if it can be brought into a conformation (staggered or eclipsed) that has a plane of symmetry (such as 27) or is identical with its mirror image.
As expected from our previous discussions diastereomers of tartaric acid have different physical properties (Table 5-2).
If you find yourself confused about the D,L and meso forms of tartaric acid, a simple analogy may help keep matters straight. Consider three sets of shoes. A right shoe beside a left shoe is a meso combination with a plane of symmetry. A left shoe next to a left shoe is not identical with, but is

the mirror image of, a right shoe next to a right shoe. None of the three combinations are identical. Each right or left shoe corresponds to a right or left configuration of a tartaric acid carbon so the three sets correspond to meso-, L-, and D-tartaric acid, respectively.
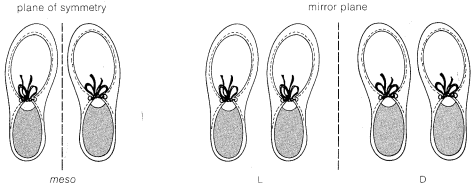
There is another symmetry test for meso configurations that is applicable to staggered conformations and can be illustrated with the tartaric acids. If you make models of 25a and 26a you will find that they are mirror images and identical but, as we have said, they have no plane of symmetry. In this conformation, the molecules do have a center of symmetry. Thus a line drawn at any angle through the midpoint of the central C−C bond of 25a (or 26a) has an identical environment on each side of the midpoint. Another way of putting it is that each half of the molecule is the photographic image (i.e., reverse) of the other half. For a molecule with chiral centers, if its projection formula has a plane of symmetry or if we can find a rotational conformation with either a plane or center of symmetry, then it will be meso and achiral.
The idea that for every nn chiral centers there can be 2n different configurations will be true only if none of the configurations has sufficient symmetry to be identical with its mirror image. For every meso form there will be one less pair of enantiomers and one less total number of possible configurations than is theoretically possible according to the number of chiral centers. At most, one meso compounds is possible for structures with four chiral centers. An example is offered by the meso forms of tetrahydroxyhexanedioic acid which, with four chiral atoms, have configurations 28 and 29:
The same information can be obtained from projection formulas. You can see that projections 19 and 20 are mirror images and that 20, 21, or 22 can not be superimposed on 19. However, in some situations confusion can result in making such comparisons and it is important to be able to translate the projection formulas into ball-and-stick models or perspective drawings


|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|