Simulated Annealing

There are certain optimization problems that become unmanageable using combinatorial methods as the number of objects becomes large. A typical example is the traveling salesman problem, which belongs to the NP-complete class of problems. For these problems, there is a very effective practical algorithm called simulated annealing (thus named because it mimics the process undergone by misplaced atoms in a metal when its heated and then slowly cooled). While this technique is unlikely to find the optimum solution, it can often find a very good solution, even in the presence of noisy data.

The traveling salesman problem can be used as an example application of simulated annealing. In this problem, a salesman must visit some large number of cities while minimizing the total mileage traveled. If the salesman starts with a random itinerary, he can then pairwise trade the order of visits to cities, hoping to reduce the mileage with each exchange. The difficulty with this approach is that while it rapidly finds a local minimum, it cannot get from there to the global minimum.

Simulated annealing improves this strategy through the introduction of two tricks. The first is the so-called "Metropolis algorithm" (Metropolis et al. 1953), in which some trades that do not lower the mileage are accepted when they serve to allow the solver to "explore" more of the possible space of solutions. Such "bad" trades are allowed using the criterion that

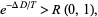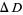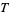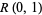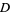where  is the change of distance implied by the trade (negative for a "good" trade; positive for a "bad" trade),  is a "synthetic temperature," and  is a random number in the interval .  is called a "cost function," and corresponds to the free energy in the case of annealing a metal (in which case the temperature parameter would actually be the 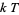, where  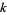is Boltzmann's Constant and  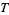is the physical temperature, in the Kelvin absolute temperature scale). If  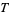is large, many "bad" trades are accepted, and a large part of solution space is accessed. Objects to be traded are generally chosen randomly, though more sophisticated techniques can be used.

The second trick is, again by analogy with annealing of a metal, to lower the "temperature." After making many trades and observing that the cost function declines only slowly, one lowers the temperature, and thus limits the size of allowed "bad" trades. After lowering the temperature several times to a low value, one may then "quench" the process by accepting only "good" trades in order to find the local minimum of the cost function. There are various "annealing schedules" for lowering the temperature, but the results are generally not very sensitive to the details.

There is another faster strategy called threshold acceptance (Dueck and Scheuer 1990). In this strategy, all good trades are accepted, as are any bad trades that raise the cost function by less than a fixed threshold. The threshold is then periodically lowered, just as the temperature is lowered in annealing. This eliminates exponentiation and random number generation in the Boltzmann criterion. As a result, this approach can be faster in computer simulations. Simulated annealing is implemented as NMinimize[f, vars, Method -> "SimulatedAnnealing"].

REFERENCES:

Dueck, G. and Scheuer, T. "Threshold Accepting: A General Purpose Optimization Algorithm Appearing Superior to Simulated Annealing." J. Comp. Phys. 90, 161-175, 1990.

Ingber, L. "Simulated Annealing: Practice Versus Theory." Math. Comput. Modelling 18, 29-57, 1993.

Kirkpatrick, S.; Gelatt, C. D.; and Vecchi, M. P. "Optimization by Simulated Annealing." Science 220, 671-680, 1983.

Metropolis, N.; Rosenbluth, A. W.; Rosenbluth, M.; Teller, A. H.; and Teller, E. "Equation of State Calculations by Fast Computing Machines." J. Chem. Phys. 21, 1087-1092, 1953.

Otten, R. H. J. M. and van Ginneken, L. P. P. P. The Annealing Algorithm. Boston, MA: Kluwer, 1989.