Interior Point Method

An interior point method is a linear or nonlinear programming method (Forsgren et al. 2002) that achieves optimization by going through the middle of the solid defined by the problem rather than around its surface.

A polynomial time linear programming algorithm using an interior point method was found by Karmarkar (1984). Arguably, interior point methods were known as early as the 1960s in the form of the barrier function methods, but the media hype accompanying Karmarkar's announcement led to these methods receiving a great deal of attention. However, it should be noted that while Karmarkar claimed that his implementation was much more efficient than the simplex method, the potential of interior point method was established only later. By 1994, there were more than 1300 published papers on interior point methods.

Current efficient implementations are mostly based on a predictor-corrector technique (Mehrotra 1992), where the Cholesky decomposition of the normal equation or 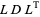 factorization of the symmetric indefinite system augmented system is used to perform Newton's method (together with some heuristics to estimate the penalty parameter). All current interior point methods implementations rely heavily on very efficient code for factoring sparse symmetric matrices.

REFERENCES:

Forsgren, A.; Gill, P. E.; and Wright, M. H. "Interior Methods for Nonlinear Optimization." SIAM Rev. 44, 525-597, 2002.

Karmarkar, N. "A New Polynomial-Time Algorithm for Linear Programming." Combinatorica 4, 373-395, 1984.

Lustig, I. J.; Marsten, R. E.; and Shanno, D. F. "Computational Experience with a Primal-Dual Interior Point Method for Linear Programming." Linear Alg. Appl. 152, 191-222, 1991.

Mehrotra, S. "On the Implementation of a Primal-Dual Interior Point Method." SIAM J. Optimization 2, 575-601, 1992.

Wright, S. J. Primal-Dual Interior-Point Methods. Philadelphia, PA: SIAM, 1997.