
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-11-2021
Date: 14-9-2021
Date: 16-2-2016
|
Neville's algorithm is an interpolation algorithm which proceeds by first fitting a polynomial of degree 0 through the point 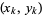 for
for 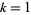 , ...,
, ..., 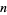 , i.e.,
, i.e., 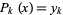 . A second iteration is then performed in which
. A second iteration is then performed in which 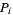 and
and 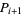 are combined to fit through pairs of points, yielding
are combined to fit through pairs of points, yielding 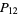 ,
, 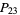 , .... The procedure is repeated, generating a "pyramid" of approximations until the final result is reached
, .... The procedure is repeated, generating a "pyramid" of approximations until the final result is reached
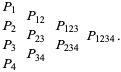 |
The final result is
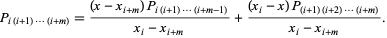 |



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|