
Cubic Spline
 المؤلف:
Bartels, R. H.; Beatty, J. C.; and Barsky, B. A
المؤلف:
Bartels, R. H.; Beatty, J. C.; and Barsky, B. A
 المصدر:
"Hermite and Cubic Spline Interpolation." Ch. 3 in An Introduction to Splines for Use in Computer Graphics and Geometric Modelling. San Francisco, CA: Morgan Kaufmann
المصدر:
"Hermite and Cubic Spline Interpolation." Ch. 3 in An Introduction to Splines for Use in Computer Graphics and Geometric Modelling. San Francisco, CA: Morgan Kaufmann
 الجزء والصفحة:
...
الجزء والصفحة:
...
 19-11-2021
19-11-2021
 2191
2191
Cubic Spline

A cubic spline is a spline constructed of piecewise third-order polynomials which pass through a set of 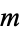 control points. The second derivative of each polynomial is commonly set to zero at the endpoints, since this provides a boundary condition that completes the system of
control points. The second derivative of each polynomial is commonly set to zero at the endpoints, since this provides a boundary condition that completes the system of 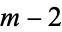 equations. This produces a so-called "natural" cubic spline and leads to a simple tridiagonal system which can be solved easily to give the coefficients of the polynomials. However, this choice is not the only one possible, and other boundary conditions can be used instead.
equations. This produces a so-called "natural" cubic spline and leads to a simple tridiagonal system which can be solved easily to give the coefficients of the polynomials. However, this choice is not the only one possible, and other boundary conditions can be used instead.
Cubic splines are implemented in the Wolfram Language as BSplineCurve[pts, SplineDegree -> 3].
Consider 1-dimensional spline for a set of 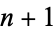 points
points 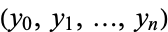 . Following Bartels et al. (1998, pp. 10-13), let the
. Following Bartels et al. (1998, pp. 10-13), let the 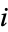 th piece of the spline be represented by
th piece of the spline be represented by
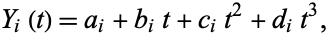 |
(1)
|
where 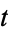 is a parameter
is a parameter ![t in [0,1]](https://mathworld.wolfram.com/images/equations/CubicSpline/Inline7.gif) and
and 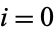 , ...,
, ..., 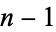 . Then
. Then
Taking the derivative of 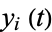 in each interval then gives
in each interval then gives
Solving (2)-(5) for 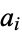 ,
, 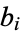 ,
, 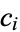 , and
, and 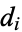 then gives
then gives
Now require that the second derivatives also match at the points, so
for interior points, as well as that the endpoints satisfy
This gives a total of 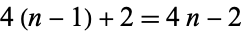 equations for the
equations for the 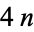 unknowns. To obtain two more conditions, require that the second derivatives at the endpoints be zero, so
unknowns. To obtain two more conditions, require that the second derivatives at the endpoints be zero, so
Rearranging all these equations (Bartels et al. 1998, pp. 12-13) leads to the following beautifully symmetric tridiagonal system
![[2 1 ; 1 4 1 ; 1 4 1 ; 1 4 1 ; | ... ... ... ... ... ...; 1 4 1; 1 2][D_0; D_1; D_2; D_3; |; D_(n-1); D_n]=[3(y_1-y_0); 3(y_2-y_0); 3(y_3-y_1); |; 3(y_(n-1)-y_(n-3)); 3(y_n-y_(n-2)); 3(y_n-y_(n-1))].](https://mathworld.wolfram.com/images/equations/CubicSpline/NumberedEquation2.gif) |
(18)
|
If the curve is instead closed, the system becomes
![[4 1 1; 1 4 1 ; 1 4 1 ; 1 4 1 ; | ... ... ... ... ... ...; 1 4 1; 1 1 4][D_0; D_1; D_2; D_3; |; D_(n-1); D_n]=[3(y_1-y_n); 3(y_2-y_0); 3(y_3-y_1); |; 3(y_(n-1)-y_(n-3)); 3(y_n-y_(n-2)); 3(y_0-y_(n-1))].](https://mathworld.wolfram.com/images/equations/CubicSpline/NumberedEquation3.gif) |
(19)
|
REFERENCES:
Bartels, R. H.; Beatty, J. C.; and Barsky, B. A. "Hermite and Cubic Spline Interpolation." Ch. 3 in An Introduction to Splines for Use in Computer Graphics and Geometric Modelling. San Francisco, CA: Morgan Kaufmann, pp. 9-17, 1998.
Burden, R. L.; Faires, J. D.; and Reynolds, A. C. Numerical Analysis, 6th ed. Boston, MA: Brooks/Cole, pp. 120-121, 1997.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. "Cubic Spline Interpolation." §3.3 in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 107-110, 1992.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


