


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-9-2021
Date: 16-8-2021
Date: 3-10-2021
|
Jackson's theorem is a statement about the error 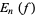 of the best uniform approximation to a real function
of the best uniform approximation to a real function 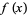 on
on ![[-1,1]](https://mathworld.wolfram.com/images/equations/JacksonsTheorem/Inline3.gif) by real polynomials of degree at most
by real polynomials of degree at most 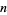 . Let
. Let 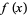 be of bounded variation in
be of bounded variation in ![[-1,1]](https://mathworld.wolfram.com/images/equations/JacksonsTheorem/Inline6.gif) and let
and let 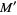 and
and 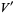 denote the least upper bound of
denote the least upper bound of 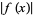 and the total variation of
and the total variation of 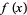 in
in ![[-1,1]](https://mathworld.wolfram.com/images/equations/JacksonsTheorem/Inline11.gif) , respectively. Given the function
, respectively. Given the function
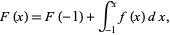 |
(1) |
then the coefficients
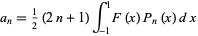 |
(2) |
of its Fourier-Legendre series, where 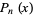 is a Legendre polynomial, satisfy the inequalities
is a Legendre polynomial, satisfy the inequalities
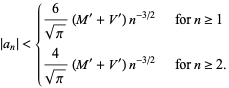 |
(3) |
Moreover, the Fourier-Legendre series of 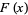 converges uniformly and absolutely to
converges uniformly and absolutely to 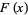 in
in ![[-1,1]](https://mathworld.wolfram.com/images/equations/JacksonsTheorem/Inline15.gif) .
.
Bernstein (1913) strengthened Jackson's theorem to
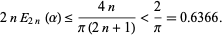 |
(4) |
A specific application of Jackson's theorem shows that if
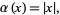 |
(5) |
then
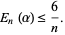 |
(6) |
REFERENCES:
Bernstein, S. N. "Sur la meilleure approximation de 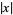 par les polynomes de degrés donnés." Acta Math. 37, 1-57, 1913.
par les polynomes de degrés donnés." Acta Math. 37, 1-57, 1913.
Cheney, E. W. Introduction to Approximation Theory, 2nd ed. Providence, RI: Amer. Math. Soc., 1999.
Finch, S. R. "Lebesgue Constants." §4.2 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 250-255, 2003.
Jackson, D. The Theory of Approximation. New York: Amer. Math. Soc., p. 76, 1930.
Korneīĭčuk, N. P. "The Exact Constant in D. Jackson's Theorem on Best Uniform Approximation of Continuous Periodic Functions." Dokl. Akad. Nauk 145, 514-515, 1962.
Rivlin, T. J. An Introduction to the Approximation of Functions. New York: Dover, 1981.
Sansone, G. Orthogonal Functions, rev. English ed. New York: Dover, pp. 205-208, 1991.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|