المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Logistic Map--r=-2 |
 1023
 04:01 مساءً
date: 1-9-2021 |
Author : MathPages 
Book or Source : "Closed Forms for the Logistic Map." http://www.mathpages.com/home/kmath188.htm. 
Page and Part : ...|
Read More
Date: 12-11-2021
1005
Date: 18-10-2021
1392
Date: 25-11-2021
1281
|
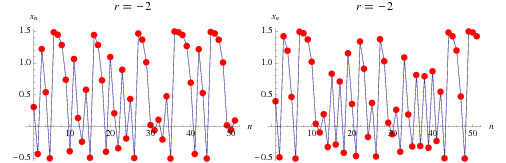
With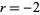 
, the logistic map becomes
 |
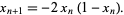(1) |
The first 50 iterations of this map are illustrated above for initial values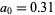 
and 0.4.
The solution can be written in the form
![x_n=1/2{1-f[r^nf^(-1)(1-2x_0)]},](https://mathworld.wolfram.com/images/equations/LogisticMapR=-2/NumberedEquation2.gif) |
(2) |
with
 |
 |
 |
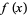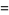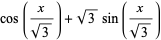(3) |
 |
 |
 |
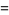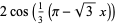(4) |
and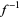 
its inverse function (Wolfram 2002, p. 1098). Explicitly, this then gives the formula
![x_n=1/2-cos{1/3[pi-(-2)^n(pi-3cos^(-1)(1/2-x_0))]}.](https://mathworld.wolfram.com/images/equations/LogisticMapR=-2/NumberedEquation3.gif) |
(5) |
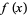has the Maclaurin series
 |
 |
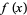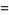![sum_(n=0)^(infty)(3^(-n/2))/(n!)[cos(1/2npi)+sqrt(3)sin(1/2pin)]](https://mathworld.wolfram.com/images/equations/LogisticMapR=-2/Inline13.gif) |
(6) |
 |
 |
 |
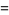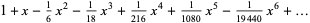(7) |
(OEIS A059944).
REFERENCES:
MathPages. "Closed Forms for the Logistic Map." http://www.mathpages.com/home/kmath188.htm.
Sloane, N. J. A. Sequence A059944 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1098, 2002.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
