Monty Hall Problem

The Monty Hall problem is named for its similarity to the Let's Make a Deal television game show hosted by Monty Hall. The problem is stated as follows. Assume that a room is equipped with three doors. Behind two are goats, and behind the third is a shiny new car. You are asked to pick a door, and will win whatever is behind it. Let's say you pick door 1. Before the door is opened, however, someone who knows what's behind the doors (Monty Hall) opens one of the other two doors, revealing a goat, and asks you if you wish to change your selection to the third door (i.e., the door which neither you picked nor he opened). The Monty Hall problem is deciding whether you do.

The correct answer is that you do want to switch. If you do not switch, you have the expected 1/3 chance of winning the car, since no matter whether you initially picked the correct door, Monty will show you a door with a goat. But after Monty has eliminated one of the doors for you, you obviously do not improve your chances of winning to better than 1/3 by sticking with your original choice. If you now switch doors, however, there is a 2/3 chance you will win the car (counterintuitive though it seems).

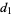		winning probability
pick	stick	1/3
pick	switch	2/3

The Season 1 episode "Man Hunt" (2005) of the television crime drama NUMB3RS mentions the Monty Hall problem.

The problem can be generalized to four doors as follows. Let one door conceal the car, with goats behind the other three. Pick a door 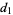. Then the host will open one of the nonwinners and give you the option of switching. Call your new choice (which could be the same as  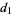if you don't switch) 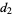. The host will then open a second nonwinner, and you must decide for choice  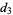if you want to stick to  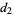or switch to the remaining door. The probabilities of winning are shown below for the four possible strategies.

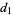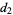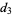			winning probability
pick	stick	stick	2/8
pick	switch	stick	3/8
pick	stick	switch	6/8
pick	switch	switch	5/8

The above results are characteristic of the best strategy for the 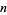-stage Monty Hall problem: stick until the last choice, then switch.

REFERENCES:

Barbeau, E. "The Problem of the Car and Goats." College Math. J. 24, 149, 1993.

Bogomolny, A. "Monty Hall Dilemma." http://www.cut-the-knot.org/hall.shtml.

Dewdney, A. K. 200% of Nothing. New York: Wiley, 1993.

Donovan, D. "The WWW Tackles the Monty Hall Problem." http://math.rice.edu/~ddonovan/montyurl.html.

Ellis, K. M. "The Monty Hall Problem." http://montyhallproblem.com/.

Flannery, S. and Flannery, D. In Code: A Mathematical Journey. London: Profile Books, pp. 135 and 244-245, 2000.

Gardner, M. Aha! Gotcha: Paradoxes to Puzzle and Delight. New York: W. H. Freeman, 1982.

Gillman, L. "The Car and the Goats." Amer. Math. Monthly 99, 3, 1992.

Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 233-240, 1998.

Neuwirth, E. "The Monty Hall Problem Put to Rest." College Math. J. 30, 369, 1999.

Selvin, S. "A Problem in Probability." Amer. Stat. 29, 67, 1975.

vos Savant, M. The Power of Logical Thinking. New York: St. Martin's Press, 1996.