


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-10-2021
Date: 23-12-2021
Date: 13-9-2021
|
The Kubo-Martin-Schwinger (KMS) condition is a kind of boundary-value condition which naturally emerges in quantum statistical mechanics and related areas.
Given a quantum system 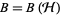 with finite dimensional Hilbert space
with finite dimensional Hilbert space 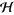 , define the function
, define the function 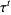 as
as
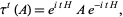 |
(1) |
where 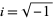 is the imaginary unit and where
is the imaginary unit and where 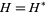 is the Hamiltonian, i.e., the sum of the kinetic energies of all the particles in
is the Hamiltonian, i.e., the sum of the kinetic energies of all the particles in 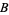 plus the potential energy of the particles associated with
plus the potential energy of the particles associated with 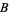 . Next, for any real number
. Next, for any real number 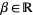 , define the thermal equilibrium
, define the thermal equilibrium 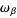 as
as
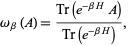 |
(2) |
where 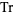 denotes the matrix trace. From
denotes the matrix trace. From 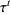 and
and 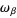 , one can define the so-called equilibrium correlation function
, one can define the so-called equilibrium correlation function 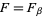 where
where
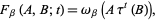 |
(3) |
whereby the KMS boundary condition says that
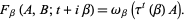 |
(4) |
In particular, this identity relates to the state 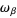 the values of the analytic function
the values of the analytic function 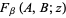 on the boundary of the strip
on the boundary of the strip
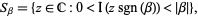 |
(5) |
where here, 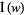 denotes the imaginary part of
denotes the imaginary part of 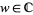 and
and 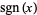 denotes the signum function applied to
denotes the signum function applied to 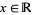 .
.
In various literature, the KMS boundary condition is stated in sometimes-different contexts. For example, the identity () is sometimes written with respect to integration, yielding
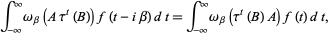 |
(6) |
where here, 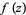 is used as shorthand for
is used as shorthand for 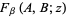 . In other literature (e.g., Araki and Miyata 1968), the condition looks different still.
. In other literature (e.g., Araki and Miyata 1968), the condition looks different still.
REFERENCES:
Araki, H. and Miyata, H. "On KMS Boundary Condition." Publ. RIMS, Kyoto Univ. Ser. A 4, 373-385, 1968.
Cohen, J. S.; Daniëls, H. A. M.; and Winnink, M. "On Generalizations of the KMS-Boundary Condition." Commun. Math. Phys. 84, 449-458, 1982.
Derezński, J. and Pillet, C. "KMS States." http://pillet.univ-tln.fr/data/pdf/KMS-states.pdf.
Nave, C. R. "The Hamiltonian in Quantum Mechanics." HyperPhysics. 2012. http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hamil.html.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|