
Lyapunov Characteristic Exponent
 المؤلف:
Ramasubramanian, K. and Sriram, M. S.
المؤلف:
Ramasubramanian, K. and Sriram, M. S.
 المصدر:
"A Comparative Study of Computation of Lyapunov Spectra with Different Algorithms" 1999. http://arxiv.org/abs/chao-dyn/9909029.
المصدر:
"A Comparative Study of Computation of Lyapunov Spectra with Different Algorithms" 1999. http://arxiv.org/abs/chao-dyn/9909029.
 الجزء والصفحة:
...
الجزء والصفحة:
...
 11-10-2021
11-10-2021
 1835
1835
Lyapunov Characteristic Exponent
The Lyapunov characteristic exponent [LCE] gives the rate of exponential divergence from perturbed initial conditions. To examine the behavior of an orbit around a point 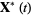 , perturb the system and write
, perturb the system and write
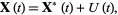 |
(1)
|
where 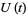 is the average deviation from the unperturbed trajectory at time
is the average deviation from the unperturbed trajectory at time 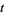 . In a chaotic region, the LCE
. In a chaotic region, the LCE 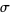 is independent of
is independent of 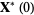 . It is given by the Oseledec theorem, which states that
. It is given by the Oseledec theorem, which states that
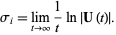 |
(2)
|
For an 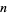 -dimensional mapping, the Lyapunov characteristic exponents are given by
-dimensional mapping, the Lyapunov characteristic exponents are given by
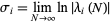 |
(3)
|
for 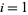 , ...,
, ..., 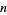 , where
, where 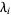 is the Lyapunov characteristic number.
is the Lyapunov characteristic number.
One Lyapunov characteristic exponent is always 0, since there is never any divergence for a perturbed trajectory in the direction of the unperturbed trajectory. The larger the LCE, the greater the rate of exponential divergence and the wider the corresponding separatrix of the chaotic region. For the standard map, an analytic estimate of the width of the chaotic zone by Chirikov (1979) finds
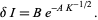 |
(4)
|
Since the Lyapunov characteristic exponent increases with increasing 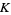 , some relationship likely exists connecting the two. Let a trajectory (expressed as a map) have initial conditions
, some relationship likely exists connecting the two. Let a trajectory (expressed as a map) have initial conditions 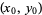 and a nearby trajectory have initial conditions
and a nearby trajectory have initial conditions 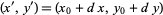 . The distance between trajectories at iteration
. The distance between trajectories at iteration 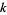 is then
is then
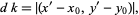 |
(5)
|
and the mean exponential rate of divergence of the trajectories is defined by
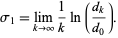 |
(6)
|
For an 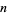 -dimensional phase space (map), there are
-dimensional phase space (map), there are 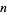 Lyapunov characteristic exponents
Lyapunov characteristic exponents 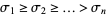 . However, because the largest exponent
. However, because the largest exponent 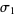 will dominate, this limit is practically useful only for finding the largest exponent. Numerically, since
will dominate, this limit is practically useful only for finding the largest exponent. Numerically, since 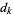 increases exponentially with
increases exponentially with 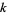 , after a few steps the perturbed trajectory is no longer nearby. It is therefore necessary to renormalize frequently every
, after a few steps the perturbed trajectory is no longer nearby. It is therefore necessary to renormalize frequently every 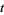 steps. Defining
steps. Defining
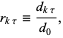 |
(7)
|
one can then compute
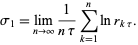 |
(8)
|
Numerical computation of the second (smaller) Lyapunov exponent may be carried by considering the evolution of a two-dimensional surface. It will behave as
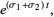 |
(9)
|
so 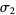 can be extracted if
can be extracted if 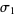 is known. The process may be repeated to find smaller exponents.
is known. The process may be repeated to find smaller exponents.
For Hamiltonian systems, the LCEs exist in additive inverse pairs, so if 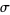 is an LCE, then so is
is an LCE, then so is 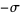 . One LCE is always 0. For a one-dimensional oscillator (with a two-dimensional phase space), the two LCEs therefore must be
. One LCE is always 0. For a one-dimensional oscillator (with a two-dimensional phase space), the two LCEs therefore must be 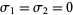 , so the motion is quasiperiodic and cannot be chaotic. For higher order Hamiltonian systems, there are always at least two 0 LCEs, but other LCEs may enter in plus-and-minus pairs
, so the motion is quasiperiodic and cannot be chaotic. For higher order Hamiltonian systems, there are always at least two 0 LCEs, but other LCEs may enter in plus-and-minus pairs 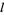 and
and 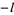 . If they, too, are both zero, the motion is integrable and not chaotic. If they are nonzero, the positive LCE
. If they, too, are both zero, the motion is integrable and not chaotic. If they are nonzero, the positive LCE 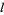 results in an exponential separation of trajectories, which corresponds to a chaotic region. Notice that it is not possible to have all LCEs negative, which explains why convergence of orbits is never observed in Hamiltonian systems.
results in an exponential separation of trajectories, which corresponds to a chaotic region. Notice that it is not possible to have all LCEs negative, which explains why convergence of orbits is never observed in Hamiltonian systems.
Now consider a dissipative system. For an arbitrary 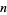 -dimensional phase space, there must always be one LCE equal to 0, since a perturbation along the path results in no divergence. The LCEs satisfy
-dimensional phase space, there must always be one LCE equal to 0, since a perturbation along the path results in no divergence. The LCEs satisfy 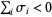 . Therefore, for a two-dimensional phase space of a dissipative system,
. Therefore, for a two-dimensional phase space of a dissipative system, 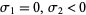 . For a three-dimensional phase space, there are three possibilities:
. For a three-dimensional phase space, there are three possibilities:
1. (Integrable): 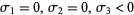 ,
,
2. (Integrable): 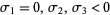 ,
,
3. (Chaotic): 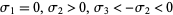 .
.
REFERENCES:
Sandri, M. "Numerical Calculation of Lyapunov Exponents." Mathematica J. 6, 78-84, 1996. http://library.wolfram.com/infocenter/Articles/2902/.
Chirikov, B. V. "A Universal Instability of Many-Dimensional Oscillator Systems." Phys. Rep. 52, 264-379, 1979.
Ramasubramanian, K. and Sriram, M. S. "A Comparative Study of Computation of Lyapunov Spectra with Different Algorithms" 1999. http://arxiv.org/abs/chao-dyn/9909029.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, p. 24, 2004. http://www.mathematicaguidebooks.org/.
 الاكثر قراءة في الرياضيات التطبيقية
الاكثر قراءة في الرياضيات التطبيقية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


