


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-10-2021
Date: 18-11-2021
Date: 4-11-2021
|
Let 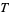 be an ergodic endomorphism of the probability space
be an ergodic endomorphism of the probability space 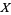 and let
and let 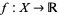 be a real-valued measurable function. Then for almost every
be a real-valued measurable function. Then for almost every 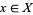 , we have
, we have
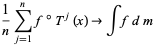 |
(1) |
as 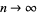 . To illustrate this, take
. To illustrate this, take 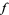 to be the characteristic function of some subset
to be the characteristic function of some subset 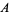 of
of 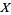 so that
so that
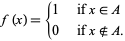 |
(2) |
The left-hand side of (1) just says how often the orbit of  (that is, the points
(that is, the points  ,
, 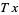 ,
, 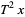 , ...) lies in
, ...) lies in 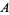 , and the right-hand side is just the measure of
, and the right-hand side is just the measure of 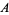 . Thus, for an ergodic endomorphism, "space-averages = time-averages almost everywhere." Moreover, if
. Thus, for an ergodic endomorphism, "space-averages = time-averages almost everywhere." Moreover, if 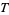 is continuous and uniquely ergodic with Borel measure
is continuous and uniquely ergodic with Borel measure 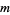 and
and 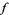 is continuous, then we can replace the almost everywhere convergence in (1) with "everywhere."
is continuous, then we can replace the almost everywhere convergence in (1) with "everywhere."
REFERENCES:
Cornfeld, I.; Fomin, S.; and Sinai, Ya. G. Appendix 3 in Ergodic Theory. New York: Springer-Verlag, 1982.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|