


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-1-2016
Date: 6-10-2021
Date: 23-12-2021
|
The definition of an Anosov map is the same as for an Anosov diffeomorphism except that instead of being a diffeomorphism, it is a map. In particular, an Anosov map is a 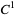 map f of a manifold
map f of a manifold 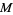 to itself such that the tangent bundle of
to itself such that the tangent bundle of 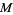 is hyperbolic with respect to
is hyperbolic with respect to 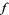 .
.
A trivial example is to map all of 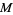 to a single point of
to a single point of 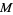 . Here, the eigenvalues are all zero. A less trivial example is an expanding map on the circle
. Here, the eigenvalues are all zero. A less trivial example is an expanding map on the circle 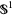 , e.g.,
, e.g., 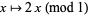 , where
, where 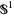 is identified with the real numbers (mod 1). Here, all the eigenvalues equal 2 (i.e., the eigenvalue at each point of
is identified with the real numbers (mod 1). Here, all the eigenvalues equal 2 (i.e., the eigenvalue at each point of 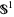 ). Note that this map is not a diffeomorphism because
). Note that this map is not a diffeomorphism because 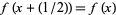 , so it has no inverse.
, so it has no inverse.
A nontrivial example is formed by taking Arnold's cat map on the 2-torus 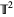 , and crossing it with an expanding map on
, and crossing it with an expanding map on 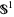 to form an Anosov map on the 3-torus
to form an Anosov map on the 3-torus 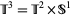 , where
, where 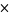 denotes the Cartesian product. In other words,
denotes the Cartesian product. In other words,
![[x_(n+1); y_(n+1); z_(n+1)]=[1 1 0; 1 2 0; 0 0 2][x_n; y_n; z_n] (mod 1).](https://mathworld.wolfram.com/images/equations/AnosovMap/NumberedEquation1.gif) |
REFERENCES:
Anosov, D. "Roughness of Geodesic Flows on Compact Riemannian Manifolds of Negative Curvature." Dokl. Akad. Nauk SSSR 145, 707-709, 1962. English translation in Soviet Math. Dokl. 3, 1068-1069, 1962.
Anosov, D. "Ergodic Properties of Geodesic Flows on Closed Riemannian Manifolds of Negative Curvature." Dokl. Akad. Nauk SSSR 151, 1250-1252, 1963. English translated in Soviet Math. Dokl. 4, 1153-1156, 1963.
Lichtenberg, A. J. and Lieberman, M. A. Regular and Chaotic Dynamics, 2nd ed. New York: Springer-Verlag, pp. 305-307, 1992.
Sondow, J. "Fixed Points of Anosov Maps of Certain Manifolds." Proc. Amer. Math. Soc. 61, 381-384, 1976.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|