Kolmogorov Entropy
المؤلف:
Ott, E
المصدر:
Chaos in Dynamical Systems. New York: Cambridge University Press
الجزء والصفحة:
...
31-8-2021
1346
Kolmogorov Entropy
Also known as metric entropy. Divide phase space into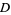 
-dimensional hypercubes of content 
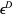. Let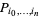 
be the probability that a trajectory is in hypercube 
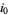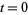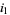at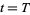 
, 
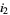at 
, 
at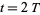 
, etc. Then define
 |
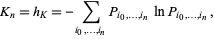(1)
|
where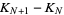 
is the information needed to predict which hypercube the trajectory will be in at 
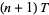given trajectories up to 
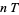. The Kolmogorov entropy is then defined by
 |
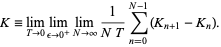(2)
|
The Kolmogorov entropy is related to Lyapunov characteristic exponents by
 |
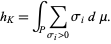(3)
|
REFERENCES:
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, p. 138, 1993.
Schuster, H. G. Deterministic Chaos: An Introduction, 3rd ed. New York: Wiley, p. 112, 1995.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
