A theorem outlined by Kolmogorov (1954) which was subsequently proved in the 1960s by Arnol'd (1963) and Moser (1962; Tabor 1989, p. 105). It gives conditions under which chaos is restricted in extent. Moser's 1962 proof was valid for twist maps

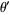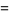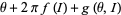			(1)
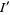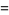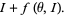			(2)

Arnol'd (1963) produced a proof for Hamiltonian systems

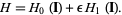(3)

The original theorem required perturbations 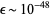, although this has since been significantly increased. Arnol'd's proof required 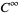, and Moser's original proof required 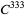. Subsequently, Moser's version has been reduced to 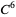, then 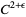, although counterexamples are known for 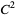. Conditions for applicability of the KAM theorem are:

1. small perturbations,

2. smooth perturbations, and

3. sufficiently irrational map winding number.

Moser considered an integrable Hamiltonian function 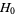 with a torus  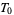and set of frequencies  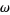having an incommensurate frequency vector  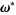(i.e.,  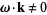for all integers 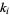). Let  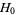be perturbed by some periodic function 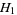. The KAM theorem states that, if  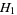is small enough, then for almost every  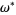there exists an invariant torus  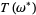of the perturbed system such that  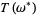is "close to" 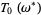. Moreover, the tori  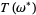form a set of positive measures whose complement has a measure which tends to zero as 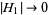. A useful paraphrase of the KAM theorem is, "For sufficiently small perturbation, almost all tori (excluding those with rational frequency vectors) are preserved." The theorem thus explicitly excludes tori with rationally related frequencies, that is,  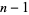conditions of the form

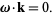(4)

These tori are destroyed by the perturbation. For a system with two degrees of freedom, the condition of closed orbits is

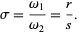(5)

For a quasiperiodic map orbit, 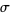 is irrational. KAM shows that the preserved tori satisfy the irrationality condition

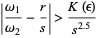(6)

for all 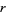 and 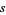, although not much is known about .

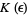The KAM theorem broke the deadlock of the small divisor problem in classical perturbation theory, and provides the starting point for an understanding of the appearance of chaos. For a Hamiltonian system, the isoenergetic nondegeneracy condition

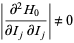(7)

guarantees preservation of most invariant tori under small perturbations 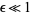. The Arnol'd version states that

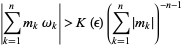(8)

for all 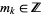. This condition is less restrictive than Moser's, so fewer points are excluded.

REFERENCES:

Arnol'd, V. I. "Proof of a Theorem of A. N. Kolmogorov on the Preservation of Conditionally Periodic Motions under a Small Perturbation of the Hamiltonian." Uspehi Mat. Nauk 18, 13-40, 1963.

Kolmogorov, A. N. "On Conservation of Conditionally Periodic Motions for a Small Change in Hamilton's Function." Dokl. Akad. Nauk SSSR 98, 527-530, 1954.

Moser, J. "On Invariant Curves of Area-Preserving Mappings of an Annulus." Nachr. Akad. Wiss. Göttingen Math.-Phys. Kl. II, 1-20, 1962.

Tabor, M. Chaos and Integrability in Nonlinear Dynamics: An Introduction. New York: Wiley, 1989.

اخر الاخبار

اخبار العتبة العباسية المقدسة

عباس.. طفل فقد والده فوجد في خدمة زائري عاشوراء وطنًا آمنًا

شعبة الخطابة النسوية تواصل إقامة مجالس العزاء في شهر المحرم الحرام

لليوم الخامس.. العتبة العباسية المقدسة تقيم مجلس عزاء في صحن مرقد أبي الفضل العباس (عليه السلام)

قسم الشؤون الفكرية يقيم مجلس عزاء حسيني في العاصمة التنزانية دار السلام

المزيد

الآخبار الصحية

لمن تجاوز الستين.. عليك بشرب 4 أكواب من القهوة يوميا ؟

الحليب مع العسل.. مزيج يمنحك 7 فوائد صحية

لا تبالغ في التنظيف.. قليل من "الاتساخ" قد يحمي عائلتك

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

المزيد

الآخبار التكنلوجية

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

المزيد