


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 25-9-2021
Date: 29-8-2021
Date: 15-12-2021
|
Consider an arbitrary one-dimensional map
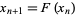 |
(1) |
(with implicit parameter 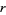 ) at the onset of chaos. After a suitable rescaling, the Feigenbaum function
) at the onset of chaos. After a suitable rescaling, the Feigenbaum function
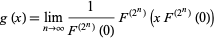 |
(2) |
is obtained. This function satisfies
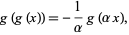 |
(3) |
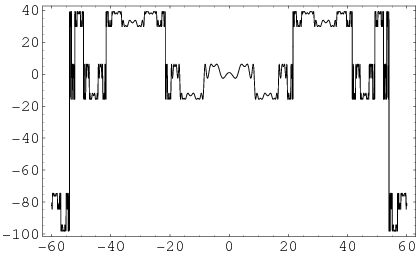
with 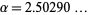 .
.
Proofs for the existence of an even analytic solution to this equation, sometimes called the Feigenbaum-Cvitanović functional equation, have been given by Campanino and Epstein (1981), Campanino et al. (1982), and Lanford (1982, 1984).
The picture above illustrate the Feigenbaum function 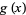 for
for 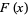 the logistic map with
the logistic map with 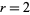 ,
,
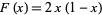 |
(4) |
along the real axis (M. Trott, pers. comm., Sept. 9, 2003).


The images above show two views of a sculpture presented by Stephen Wolfram to Mitchell Feigenbaum on the occasion of his 60th birthday that depicts the Feigenbaum function in the complex plane. The sculpture (photos courtesy of A. Young) was designed by M. Trott and laser-etched into a block of glass by Bathsheba Grossman (http://www.bathsheba.com/). The bottom view shows 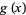 for
for  approximately between
approximately between 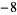 and 8.
and 8.
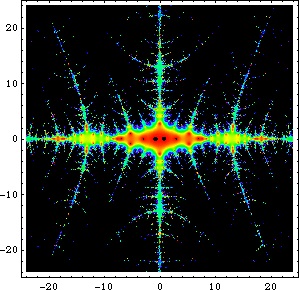
The pictures above illustrate the Feigenbaum function 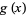 in the complex plane (M. Trott, pers. comm., Sept. 9, 2003).
in the complex plane (M. Trott, pers. comm., Sept. 9, 2003).
REFERENCES:
Campanino, M. and Epstein, H. "On the Existence of Feigenbaum's Fixed Point." Commun. Math. Phys. 79, 261-302, 1981.
Campanino, M.; Epstein, H.; and Ruelle, D. "On Feigenbaum's Functional Equation." Topology 21, 125-129, 1982.
Feigenbaum, M. J. "Quantitative Universality for a Class of Non-Linear Transformations." J. Stat. Phys. 19, 25-52, 1978.
Grassberger, P. and Procaccia, I. "Measuring the Strangeness of Strange Attractors." Physica D 9, 189-208, 1983.
Grossman, B. "Bathsheba Grossman--Laser Crystals." http://www.bathsheba.com/crystal/.
Lanford, O. E. III. "A Computer-Assisted Proof of the Feigenbaum Conjectures." Bull. Amer. Math. Soc. 6, 427-434, 1982.
Lanford, O. E. III. "A Shorter Proof of the Existence of the Feigenbaum Fixed Point." Commun. Math. Phys. 96, 521-538, 1984.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|