A two-dimensional binary (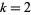) totalistic cellular automaton with a von Neumann neighborhood of range 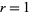. It has a birth rule that at least 2 of its 4 neighbors are alive, and a survival rule that all cells survive.  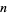steps of bootstrap percolation on an  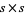grid with random initial condition of density  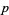can be implemented in the Wolfram Language as

With[{n = 10, p = 0.1, s = 20},
  CellularAutomaton[
    {1018, {2, {{0, 2, 0}, {2, 1, 2}, {0, 2, 0}}},
      {1, 1}},
    Table[If[Random[Real] < p, 1, 0],  {s},  {s}],
    n
  ]
]

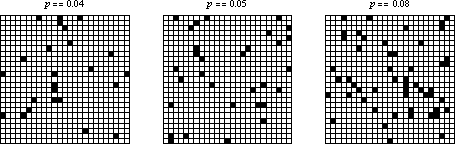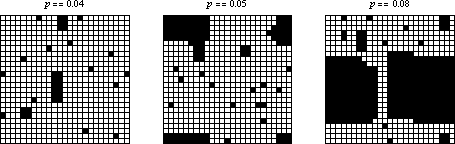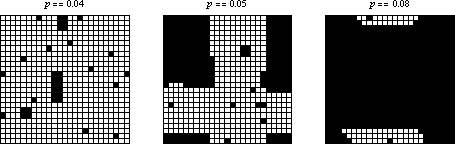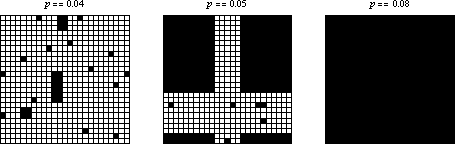
If the initial condition consists of a random sparse arrangement of cells with density 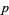, then the system seems to quickly converge to a steady state of rectangular islands of live cells surrounded by a sea of dead cells. However, as  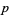crosses some threshold on finite-sized grids, the behavior appears to change so that every cell becomes live. Several examples are shown above on three  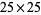grids with random initial conditions and different starting densities.

However, this conclusion proves to be incorrect, since the apparent change in behavior actually is a spurious edge effect introduced by use of a finite-sized grid. Amazingly, Holroyd (2003) showed that the asymptotic threshold occurs such that

REFERENCES:

Aizenman, M. and Lebowitz, J. "Metastability Effects in Bootstrap Percolation." J. Phys. A 21, 3801-3813, 1988.

Gray, L. "A Mathematician Looks at Wolfram's New Kind of Science." Not. Amer. Math. Soc. 50, 200-211, 2003.

Holroyd, A. "Sharp Metastability Threshold for Two-Dimensional Bootstrap Percolation." Prob. Th. and Related Fields 125, 195-224, 2003.

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 337-342, 2002.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد