Subspace

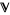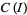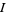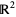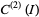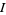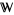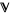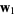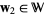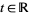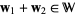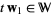Let  be a real vector space (e.g., the real continuous functions  on a closed interval , two-dimensional Euclidean space , the twice differentiable real functions  on , etc.). Then  is a real subspace of  if  is a subset of  and, for every ,  and  (the reals),  and . Let 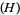 be a homogeneous system of linear equations in 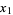, ..., 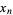. Then the subset  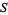of 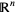 which consists of all solutions of the system  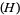is a subspace of .

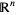More generally, let 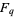 be a field with 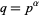, where  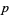is prime, and let  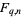denote the 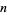-dimensional vector space over 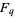. The number of 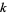-D linear subspaces of  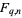is

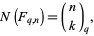(1)

where this is the q-binomial coefficient (Aigner 1979, Exton 1983). The asymptotic limit is

(2)

where

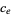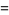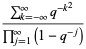			(3)
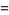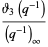			(4)
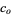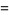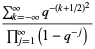			(5)
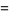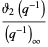			(6)

(Finch 2003), where 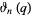 is a Jacobi theta function and  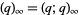is a q-Pochhammer symbol. The case  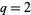gives the q-analog of the Wallis formula.

REFERENCES:

Aigner, M. Combinatorial Theory. New York: Springer-Verlag, 1979.

Exton, H. q-Hypergeometric Functions and Applications. New York: Halstead Press, 1983.

Finch, S. R. "Lengyel's Constant." Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 316-321, 2003.