
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-5-2021
Date: 4-7-2021
Date: 6-7-2021
|
A set  in a first-countable space is dense in
in a first-countable space is dense in 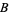 if
if 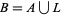 , where
, where 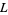 is the set of limit points of
is the set of limit points of 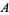 . For example, the rational numbers are dense in the reals. In general, a subset
. For example, the rational numbers are dense in the reals. In general, a subset 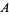 of
of 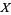 is dense if its set closure
is dense if its set closure 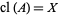 .
.
A real number 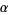 is said to be
is said to be 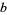 -dense iff, in the base-
-dense iff, in the base-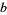 expansion of
expansion of 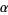 , every possible finite string of consecutive digits appears. If
, every possible finite string of consecutive digits appears. If 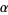 is
is 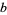 -normal, then
-normal, then 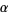 is also
is also 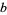 -dense. If, for some
-dense. If, for some 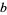 ,
, 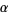 is
is 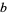 -dense, then
-dense, then 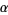 is irrational. Finally,
is irrational. Finally, 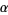 is
is 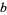 -dense iff the sequence
-dense iff the sequence 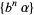 is dense (Bailey and Crandall 2001, 2003).
is dense (Bailey and Crandall 2001, 2003).
REFERENCES:
Bailey, D. H. and Crandall, R. E. "On the Random Character of Fundamental Constant Expansions." Exper. Math. 10, 175-190, 2001.
Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|