


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 4-8-2021
Date: 5-6-2021
Date: 28-6-2017
|
Calabi-Yau spaces are important in string theory, where one model posits the geometry of the universe to consist of a ten-dimensional space of the form 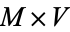 , where
, where 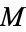 is a four dimensional manifold (space-time) and
is a four dimensional manifold (space-time) and 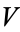 is a six dimensional compact Calabi-Yau space. They are related to Kummer surfaces. Although the main application of Calabi-Yau spaces is in theoretical physics, they are also interesting from a purely mathematical standpoint. Consequently, they go by slightly different names, depending mostly on context, such as Calabi-Yau manifolds or Calabi-Yau varieties.
is a six dimensional compact Calabi-Yau space. They are related to Kummer surfaces. Although the main application of Calabi-Yau spaces is in theoretical physics, they are also interesting from a purely mathematical standpoint. Consequently, they go by slightly different names, depending mostly on context, such as Calabi-Yau manifolds or Calabi-Yau varieties.
Although the definition can be generalized to any dimension, they are usually considered to have three complex dimensions. Since their complex structure may vary, it is convenient to think of them as having six real dimensions and a fixed smooth structure.
A Calabi-Yau space is characterized by the existence of a nonvanishing harmonic spinor 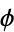 . This condition implies that its canonical bundle is trivial.
. This condition implies that its canonical bundle is trivial.
Consider the local situation using coordinates. In 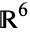 , pick coordinates
, pick coordinates 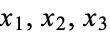 and
and 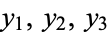 so that
so that
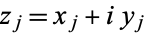 |
(1) |
gives it the structure of 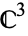 . Then
. Then
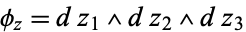 |
(2) |
is a local section of the canonical bundle. A unitary change of coordinates 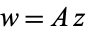 , where
, where 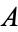 is a unitary matrix, transforms
is a unitary matrix, transforms 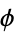 by
by 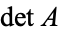 , i.e.,
, i.e.,
 |
(3) |
If the linear transformation 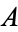 has determinant 1, that is, it is a special unitary transformation, then
has determinant 1, that is, it is a special unitary transformation, then 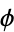 is consistently defined as
is consistently defined as 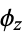 or as
or as 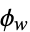 .
.
On a Calabi-Yau manifold 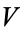 , such a
, such a 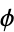 can be defined globally, and the Lie group
can be defined globally, and the Lie group 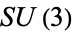 is very important in the theory. In fact, one of the many equivalent definitions, coming from Riemannian geometry, says that a Calabi-Yau manifold is a
is very important in the theory. In fact, one of the many equivalent definitions, coming from Riemannian geometry, says that a Calabi-Yau manifold is a 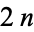 -dimensional manifold whose holonomy group reduces to
-dimensional manifold whose holonomy group reduces to 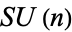 . Another is that it is a calibrated manifold with a calibration form
. Another is that it is a calibrated manifold with a calibration form 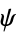 , which is algebraically the same as the real part of
, which is algebraically the same as the real part of
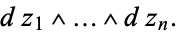 |
(4) |
Often, the extra assumptions that 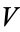 is simply connected and/or compact are made.
is simply connected and/or compact are made.
Whatever definition is used, Calabi-Yau manifolds, as well as their moduli spaces, have interesting properties. One is the symmetries in the numbers forming the Hodge diamond of a compact Calabi-Yau manifold. It is surprising that these symmetries, called mirror symmetry, can be realized by another Calabi-Yau manifold, the so-called mirror of the original Calabi-Yau manifold. The two manifolds together form a mirror pair. Some of the symmetries of the geometry of mirror pairs have been the object of recent research.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|