المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Symplectic Manifold |
 1502
 01:25 صباحاً
date: 14-7-2021 |
Author : Sjamaar, R 
Book or Source : "Symplectic Reduction and Riemann-Roch Formulas for Multiplicities." Bull. Amer. Math. Soc. 33 
Page and Part : 327-338|
Read More
Date: 10-8-2021
2026
Date: 20-6-2021
1793
Date: 16-7-2021
1153
|
A pair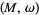 
, where 
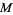is a manifold and 
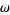is a symplectic form on 
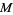. The phase space 
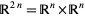is a symplectic manifold. Near every point on a symplectic manifold, it is possible to find a set of local "Darboux coordinates" in which the symplectic form has the simple form
 |
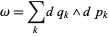(Sjamaar 1996), where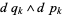 
is a wedge product.
REFERENCES:
Sjamaar, R. "Symplectic Reduction and Riemann-Roch Formulas for Multiplicities." Bull. Amer. Math. Soc. 33, 327-338, 1996.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|
