Miller Institute Knot

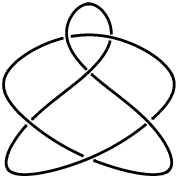The Miller Institute knot is the 6-crossing prime knot 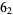. It is alternating, chiral, and invertible. A knot diagram of its laevo form is illustrated above, which is implemented in the Wolfram Language as KnotData[6, 2].

The knot is so-named because it appears on the logo of the Adolph C. and Mary Sprague Miller Institute for Basic Research in Science at the University of California, Berkeley (although, as can be seen in the logo, the Miller Institute's knot actually has dextro chirality).

The knot has braid word 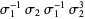. It has Arf invariant 1 and is not amphichiral, although it is invertible.

The Alexander polynomial 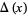, BLM/Ho polynomial 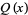, Conway polynomial 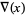, HOMFLY polynomial 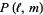, and Jones polynomial  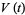of the Miller Institute knot are

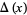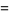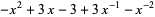			(1)
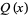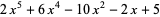			(2)
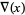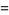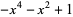			(3)
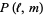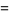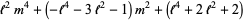			(4)
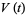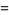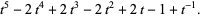			(5)

No knots on 10 or fewer crossings share the same Alexander polynomial, BLM/Ho polynomial, or Jones polynomial with the Miller Institute knot.

REFERENCES:

The Adolph C. and Mary Sprague Miller Institute for Basic Research in Science. University of California, Berkeley. https://millerinstitute.berkeley.edu/.

Bar-Natan, D. "The Knot ." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/6.2.html.

KnotPlot. "." https://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=6&id=2.